题目内容
在平面内,已知椭圆
+
=1(a>b>0)的两个焦点为F1,F2,椭圆的离心率为
,P点是椭圆上任意一点,且|PF1|+|PF2|=4,
(1)求椭圆的标准方程;
(2)以椭圆的上顶点B为直角顶点作椭圆的内接等腰直角三角形ABC,这样的等腰直角三角形是否存在?若存在请说明有几个、并求出直角边所在直线方程?若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆的标准方程;
(2)以椭圆的上顶点B为直角顶点作椭圆的内接等腰直角三角形ABC,这样的等腰直角三角形是否存在?若存在请说明有几个、并求出直角边所在直线方程?若不存在,请说明理由.
分析:(1)由题意得
,由此能求出椭圆方程.
(2)设BA的直线方程为设y=kx+1,(不妨设k>0).由
,得(1+4k2)x2+8kx=0,由此分别用k表示出AB和BC的长,再由AB=BC,求出直角边所在直线方程.
|
(2)设BA的直线方程为设y=kx+1,(不妨设k>0).由
|
解答:解:(1)由题意得
,∴
,∴b=1,
∴方程为:
+
=1.(5分)
(2)设BA的直线方程为设y=kx+1,(不妨设k>0)
由
,得(1+4k2)x2+8kx=0,
∴x1=0,x2=
,(7分)
∴A(
,
+1),
∴AB=
=
,
∴BC=
,
由AB=BC,得k(k2+4)=4k2+1,
即(k-1)(k2-3k+1)=0,即k=1或k=
所以,存在3个等腰直角三角形.
直角边所在直线方程为y=±x+1,y=
x+1,y=
x+1.…(15分)
|
|
∴方程为:
| x2 |
| 4 |
| y2 |
| 1 |
(2)设BA的直线方程为设y=kx+1,(不妨设k>0)
由
|
∴x1=0,x2=
| -8k |
| 4k2+1 |
∴A(
| -8k |
| 4k2+1 |
| -8k2 |
| 4k2+1 |
∴AB=
(
|
| 8k |
| 4k2+1 |
| k2+1 |
∴BC=
8
| ||
| k2+4 |
由AB=BC,得k(k2+4)=4k2+1,
即(k-1)(k2-3k+1)=0,即k=1或k=
3±
| ||
| 2 |
所以,存在3个等腰直角三角形.
直角边所在直线方程为y=±x+1,y=
±3+
| ||
| 2 |
±3-
| ||
| 2 |
点评:本题考查椭圆方程的求法,考查等腰直角三角形个数的判断和直角边所在直线方程的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
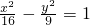 ;
;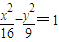 ;
;