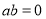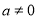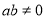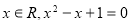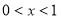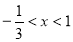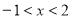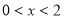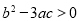题目内容
设直线 是曲线
是曲线
 的一条切线,
的一条切线, .
.
(1)求切点坐标及 的值;
的值;
(2)当 时,存在
时,存在
 ,求实数
,求实数 的取值范围.
的取值范围.
(1)切点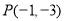 ,
,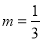 或者切点
或者切点 ,
, ;(2)
;(2) .
.
【解析】
试题分析:(1)先设切点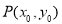 ,然后依题意计算出
,然后依题意计算出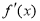 ,由
,由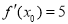 ,计算出切点的横坐标,代入切线的方程,可得切点的纵坐标,最后再将切点的坐标代入曲线C的方程计算得
,计算出切点的横坐标,代入切线的方程,可得切点的纵坐标,最后再将切点的坐标代入曲线C的方程计算得 的值;(2)结合(1)中求出的
的值;(2)结合(1)中求出的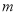 ,确定
,确定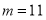 ,设
,设 ,然后将存在
,然后将存在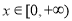 使
使 成立问题,转化为
成立问题,转化为 ,进而求出
,进而求出 ,分
,分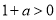 、
、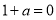 、
、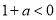 三种情况讨论函数
三种情况讨论函数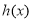 在
在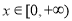 上的单调性,确定
上的单调性,确定 ,相应求解不等式
,相应求解不等式 ,即可确定
,即可确定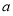 的取值范围.
的取值范围.
试题解析:(1)设直线 与曲线
与曲线 相切于点
相切于点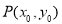
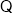
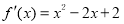 ∴
∴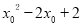
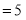 ,解得
,解得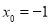 或
或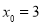
代入直线 方程,得切点
方程,得切点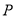 坐标为
坐标为 或
或
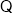 切点
切点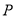 在曲线
在曲线 上,∴
上,∴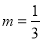 或
或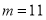
综上可知,切点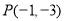 ,
,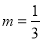 或者切点
或者切点 ,
, 5分
5分
(2)∵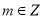 ,∴
,∴ ,设
,设 ,若存在
,若存在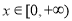 使
使 成立,则只要
成立,则只要 7分
7分

①当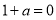 即
即 时
时
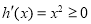 ,
, 是增函数,
是增函数,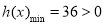 不合题意 8分
不合题意 8分
②若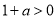 即
即
令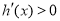 ,得
,得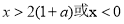 ,∴
,∴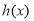 在
在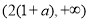 上是增函数
上是增函数
令 ,解得
,解得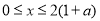 ,∴
,∴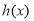 在
在 上是减函数
上是减函数

 ,
, ,解得
,解得 10分
10分
③若 即
即 ,
,
令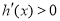 ,解得
,解得
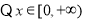 ,∴
,∴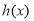 在
在 上是增函数
上是增函数
∴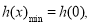
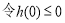 ,不等式无解,∴
,不等式无解,∴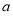 不存在 12分
不存在 12分
综上可得,实数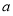 的取值范围为
的取值范围为 13分.
13分.
考点:1.导数的几何意义;2.函数的最值与导数;3.分类讨论的思想.

练习册系列答案
相关题目