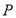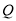题目内容
有下列命题:
① 是函数
是函数 的极值点;
的极值点;
②三次函数 有极值点的充要条件是
有极值点的充要条件是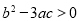 ;
;
③奇函数 在区间
在区间 上是递增的;
上是递增的;
④曲线 在
在 处的切线方程为
处的切线方程为 .
.
其中真命题的序号是 .
②③④
【解析】
试题分析:对于①,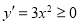 ,所以
,所以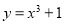 在R上单调递增,没有极值点;对于②,对于三次函数
在R上单调递增,没有极值点;对于②,对于三次函数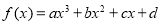 有极值点的充要条件是
有极值点的充要条件是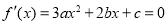 有两个不相等的实根,所以
有两个不相等的实根,所以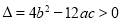 即
即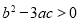 ,正确;对于③,因为函数
,正确;对于③,因为函数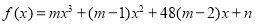 为奇函数,所以
为奇函数,所以 即
即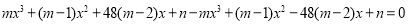 即
即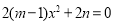 对任意
对任意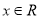 都成立,所以
都成立,所以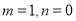 ,此时
,此时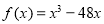 ,所以
,所以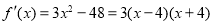 ,当
,当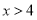 时,
时,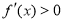 ,所以
,所以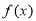 在区间
在区间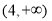 上递增;对于④,因为
上递增;对于④,因为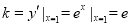 ,所以曲线
,所以曲线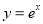 在
在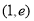 处的切线方程为
处的切线方程为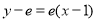 即
即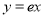 ;综上可知②③④正确.
;综上可知②③④正确.
考点:1.函数的极值与导数;2.函数的单调性与导数;3.导数的几何意义;4.充分必要条件.

练习册系列答案
相关题目