题目内容
在平面直角坐标系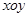 中,以
中,以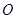 为极点,
为极点,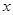 轴非负半轴为极轴建立坐标系,已知曲线
轴非负半轴为极轴建立坐标系,已知曲线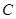 的极坐标方程为
的极坐标方程为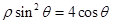 ,直线
,直线 的参数方程为:
的参数方程为: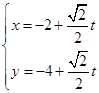 (
( 为参数),两曲线相交于
为参数),两曲线相交于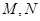 两点.
两点.
(1)写出曲线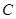 的直角坐标方程和直线
的直角坐标方程和直线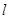 的普通方程;
的普通方程;
(2)若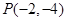 求
求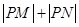 的值.
的值.
 中,以
中,以 为极点,
为极点, 轴非负半轴为极轴建立坐标系,已知曲线
轴非负半轴为极轴建立坐标系,已知曲线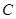 的极坐标方程为
的极坐标方程为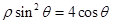 ,直线
,直线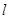 的参数方程为:
的参数方程为: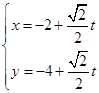 (
(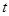 为参数),两曲线相交于
为参数),两曲线相交于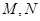 两点.
两点.(1)写出曲线
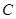 的直角坐标方程和直线
的直角坐标方程和直线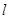 的普通方程;
的普通方程;(2)若
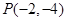 求
求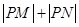 的值.
的值.(1)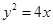 ;(2)
;(2)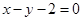
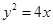 ;(2)
;(2)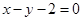
试题分析:(1)因为要将曲线
 的极坐标方程为
的极坐标方程为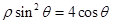 化为直角坐标方程,需要根据三个变化关系式,
化为直角坐标方程,需要根据三个变化关系式,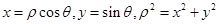 .所以在极坐标方程的两边同乘一个
.所以在极坐标方程的两边同乘一个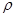 ,在根据变化关系的三个等式即可.
,在根据变化关系的三个等式即可.(2)通过判断点
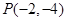 就在直线上,所以只要联立直线的参数方程与抛物线的普通方程,得到关于t的等式,利用韦达定理以,及参数方程所表示的弦长公式即可求出结论.
就在直线上,所以只要联立直线的参数方程与抛物线的普通方程,得到关于t的等式,利用韦达定理以,及参数方程所表示的弦长公式即可求出结论.试题解析:(1)(曲线C的直角坐标方程为
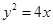 , 直线l的普通方程
, 直线l的普通方程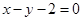 .
. (2)直线
 的参数方程为
的参数方程为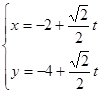 (t为参数),
(t为参数),代入y2=4x, 得到
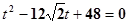 ,设M,N对应的参数分别为t1,t2
,设M,N对应的参数分别为t1,t2则
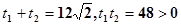
所以|PM|+|PN|=|t1+t2|=

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
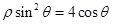 ,直线
,直线 的参数方程为
的参数方程为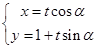 (t为参数,
(t为参数,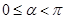 )
) 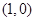 ,求直线
,求直线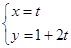 (t为参数)和圆C的极坐标方程:ρ=2
(t为参数)和圆C的极坐标方程:ρ=2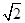 sin(θ+
sin(θ+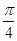 ).
).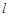 的参数方程为
的参数方程为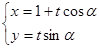 (t为参数,0<a<
(t为参数,0<a<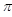 ),曲线C的极坐标方程为
),曲线C的极坐标方程为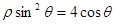 .
.
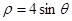 的圆心到直线
的圆心到直线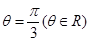 的距离是
的距离是 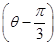 =a,a∈R,圆C的参数方程是
=a,a∈R,圆C的参数方程是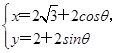 (θ为参数).若圆C关于直线l对称,则a=________.
(θ为参数).若圆C关于直线l对称,则a=________.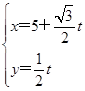 (t为参数).
(t为参数).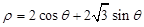 ,则圆心C的一个极坐标为 .
,则圆心C的一个极坐标为 .