题目内容
已知曲线C的极坐标方程为ρ=4cos θ,以极点为原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为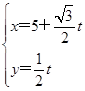 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程与直线l的普通方程;
(2)设曲线C与直线l相交于P,Q两点,以PQ为一条边作曲线C的内接矩形,求该矩形的面积.
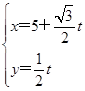 (t为参数).
(t为参数).(1)求曲线C的直角坐标方程与直线l的普通方程;
(2)设曲线C与直线l相交于P,Q两点,以PQ为一条边作曲线C的内接矩形,求该矩形的面积.
(1)x-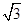 y-5=0(2)3
y-5=0(2)3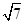
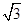 y-5=0(2)3
y-5=0(2)3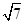
(1)由ρ=4cos θ,得ρ2=4ρcos θ,即曲线C的直角坐标方程为x2+y2=4x;
由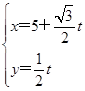 (t为参数),得y=
(t为参数),得y=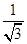 (x-5),即直线l的普通方程为x-
(x-5),即直线l的普通方程为x-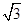 y-5=0.
y-5=0.
(2)由(1)可知C为圆,且圆心坐标为(2,0),半径为2,则弦心距d=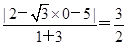 ,弦长|PQ|=2
,弦长|PQ|=2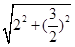 =
=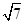 ,因此以PQ为边的圆C的内接矩形面积S=2d·|PQ|=3
,因此以PQ为边的圆C的内接矩形面积S=2d·|PQ|=3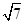
由
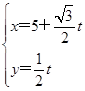 (t为参数),得y=
(t为参数),得y=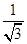 (x-5),即直线l的普通方程为x-
(x-5),即直线l的普通方程为x-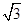 y-5=0.
y-5=0.(2)由(1)可知C为圆,且圆心坐标为(2,0),半径为2,则弦心距d=
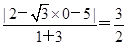 ,弦长|PQ|=2
,弦长|PQ|=2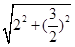 =
=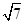 ,因此以PQ为边的圆C的内接矩形面积S=2d·|PQ|=3
,因此以PQ为边的圆C的内接矩形面积S=2d·|PQ|=3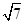

练习册系列答案
相关题目
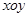 中,以
中,以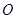 为极点,
为极点,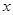 轴非负半轴为极轴建立坐标系,已知曲线
轴非负半轴为极轴建立坐标系,已知曲线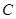 的极坐标方程为
的极坐标方程为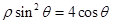 ,直线
,直线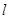 的参数方程为:
的参数方程为: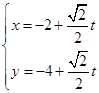 (
(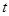 为参数),两曲线相交于
为参数),两曲线相交于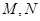 两点.
两点.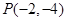 求
求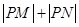 的值.
的值.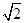 cosθ+sinθ)=1与曲线C2:ρ=a(a>0)的一个交点在极轴上,求a的值.
cosθ+sinθ)=1与曲线C2:ρ=a(a>0)的一个交点在极轴上,求a的值.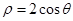 在点
在点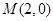 处的切线的极坐标方程为 .
处的切线的极坐标方程为 .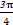 )=
)=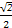 ,曲线P:ρ2-4ρcosθ+3=0,
,曲线P:ρ2-4ρcosθ+3=0,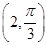 ,半径R=
,半径R=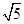 ,求圆C的极坐标方程.
,求圆C的极坐标方程.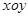 中,椭圆
中,椭圆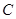 的参数方程为
的参数方程为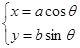 (
(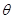 为参数,
为参数,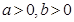 ).在极坐标系(与直角坐标系
).在极坐标系(与直角坐标系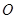 为极点,以
为极点,以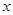 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线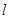 的极坐标方程为
的极坐标方程为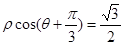 ,若直线
,若直线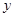 轴的交点分别是椭圆
轴的交点分别是椭圆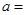 .
.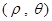 中,直线
中,直线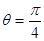 (
(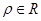 )被圆
)被圆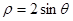 截得的弦的长是 .
截得的弦的长是 .