题目内容
椭圆 的焦点为F1,F2,两条准线与x轴的交点分别为M,N,若|MN|≤2|F1F2|,则该椭圆离心率的取值范围是
的焦点为F1,F2,两条准线与x轴的交点分别为M,N,若|MN|≤2|F1F2|,则该椭圆离心率的取值范围是
- A.
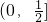
- B.

- C.
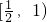
- D.

D
分析:根据准线方程公式,由椭圆的方程可得y=± ,表示出|MN|的长,又|F1F2|=2c,所以把|MN|和|F1F2|的长分别代入|MN|≤2|F1F2|,化简后即可求出e的范围,然后根据a大于c得到e小于1,两者求出交集即可得到椭圆离心率的取值范围.
,表示出|MN|的长,又|F1F2|=2c,所以把|MN|和|F1F2|的长分别代入|MN|≤2|F1F2|,化简后即可求出e的范围,然后根据a大于c得到e小于1,两者求出交集即可得到椭圆离心率的取值范围.
解答:因为椭圆的准线方程为y=± ,所以|MN|=
,所以|MN|= ;又|F1F2|=2c,
;又|F1F2|=2c,
则由|MN|≤2|F1F2|,得到 ≤4c,即
≤4c,即 ≥
≥ ,即e=
,即e= ≥
≥ ,又a>c,所以e<1,
,又a>c,所以e<1,
则该椭圆离心率的取值范围是[ ,1).
,1).
故选D
点评:此题考查学生掌握椭圆的准线方程的求法,以及灵活运用椭圆的简单性质化简求值,是一道综合题.
分析:根据准线方程公式,由椭圆的方程可得y=±
 ,表示出|MN|的长,又|F1F2|=2c,所以把|MN|和|F1F2|的长分别代入|MN|≤2|F1F2|,化简后即可求出e的范围,然后根据a大于c得到e小于1,两者求出交集即可得到椭圆离心率的取值范围.
,表示出|MN|的长,又|F1F2|=2c,所以把|MN|和|F1F2|的长分别代入|MN|≤2|F1F2|,化简后即可求出e的范围,然后根据a大于c得到e小于1,两者求出交集即可得到椭圆离心率的取值范围.解答:因为椭圆的准线方程为y=±
 ,所以|MN|=
,所以|MN|= ;又|F1F2|=2c,
;又|F1F2|=2c,则由|MN|≤2|F1F2|,得到
 ≤4c,即
≤4c,即 ≥
≥ ,即e=
,即e= ≥
≥ ,又a>c,所以e<1,
,又a>c,所以e<1,则该椭圆离心率的取值范围是[
 ,1).
,1).故选D
点评:此题考查学生掌握椭圆的准线方程的求法,以及灵活运用椭圆的简单性质化简求值,是一道综合题.

练习册系列答案
相关题目
