题目内容
(本小题满分13分)已知函数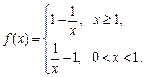
(I)当0< a < b,且f(a) = f(b)时,求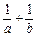 的值;
的值;
(II)若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ma,mb](m≠0).求m的取值范围.
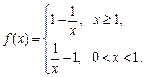
(I)当0< a < b,且f(a) = f(b)时,求
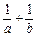 的值;
的值;(II)若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ma,mb](m≠0).求m的取值范围.
(1)
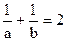
(2)
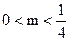
解:(I)∵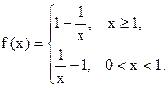
∴f(x)在(0,1)上为减函数,在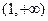 上是增函数.
上是增函数.
由0<a<b,且f(a)=f(b),可得 0<a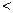 1<b且
1<b且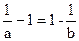 .所以
.所以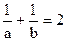 .
.
(II)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].
则a>0,m>0.
当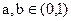 时,由于f(x)在(0,1)上是减函数,故
时,由于f(x)在(0,1)上是减函数,故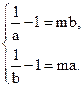 .
.
此时得a,b异号,不符合题意,所以a,b不存在.
当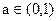
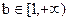 时,易知0在值域内,值域不可能是[ma,mb],所以a,b不存在. 故只有
时,易知0在值域内,值域不可能是[ma,mb],所以a,b不存在. 故只有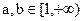 . ∵
. ∵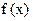 在
在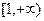 上是增函数,
上是增函数,
∴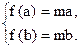 即
即 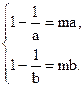 a、b是方程
a、b是方程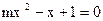 的两个根.
的两个根.
即关于x的方程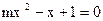 有两个大于1的实根.设这两个根为
有两个大于1的实根.设这两个根为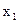 ,
,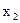 .
.
则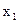 +
+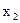 =
=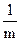 ,
,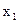 ·
·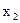 =
=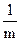 .
.
∴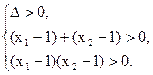 即
即 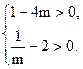 解得
解得 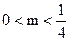 .
.
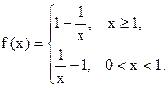
∴f(x)在(0,1)上为减函数,在
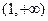 上是增函数.
上是增函数.由0<a<b,且f(a)=f(b),可得 0<a
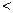 1<b且
1<b且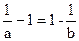 .所以
.所以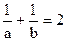 .
.(II)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].
则a>0,m>0.
当
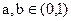 时,由于f(x)在(0,1)上是减函数,故
时,由于f(x)在(0,1)上是减函数,故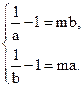 .
.此时得a,b异号,不符合题意,所以a,b不存在.
当
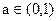
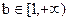 时,易知0在值域内,值域不可能是[ma,mb],所以a,b不存在. 故只有
时,易知0在值域内,值域不可能是[ma,mb],所以a,b不存在. 故只有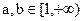 . ∵
. ∵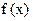 在
在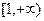 上是增函数,
上是增函数,∴
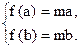 即
即 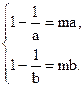 a、b是方程
a、b是方程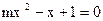 的两个根.
的两个根.即关于x的方程
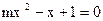 有两个大于1的实根.设这两个根为
有两个大于1的实根.设这两个根为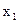 ,
,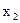 .
.则
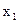 +
+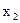 =
=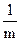 ,
,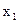 ·
·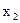 =
=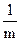 .
.∴
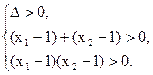 即
即 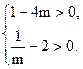 解得
解得 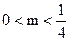 .
. 
练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
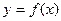 的图象关于
的图象关于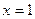 对称,当
对称,当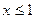 时
时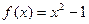 ;
;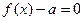 (
(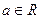 )的根的情况.
)的根的情况.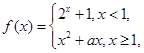 若
若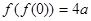 ,则实数
,则实数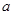 等于
等于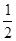
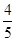
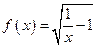 .
.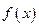 的定义域;
的定义域;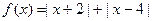 的最小值是 。
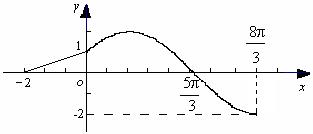
的最小值是 。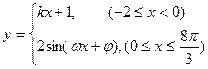 的图象如下图,则( )
的图象如下图,则( ) 



 上连续不断,定义:
上连续不断,定义: ,
, ,其中,
,其中, 表示函数
表示函数 在
在 上的最小值,
上的最小值, 表示函数
表示函数 对任意的
对任意的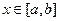 成立,则称函数
成立,则称函数 上的“
上的“ 阶收缩函数” .
阶收缩函数” . 为[-1,4]上的“
为[-1,4]上的“