题目内容

若直线（2+m）x+（m-1）y+7=0与直线（1-m）x+（3m-2）y-13=0互相垂直，则m的值为（　　）
A．1B．2C．1或0D．1或2
由于直线（2+m）x+（m-1）y+7=0与直线（1-m）x+（3m-2）y-13=0，
不妨设A1=2+m，B1=m-1，A2=1-m，B2=3m-2，
∵直线（2+m）x+（m-1）y+7=0与直线（1-m）x+（3m-2）y-13=0互相垂直，
∴A1A2+B1B2=0，即（2+m）×（1-m）+（m-1）×（3m-2）=0，
解得：m=1或2．
∴使直线（2+m）x+（m-1）y+7=0与直线（1-m）x+（3m-2）y-13=0互相垂直的m的值为1或2．
故答案为：D．
练习册系列答案
相关题目
（文）一条光线经过点P(1,3)，射在直线x+y+1=0上，反射后穿过点Q(1,1)，则这条光线从P到Q的长度为           .
过点P（1，4）作直线与两坐标轴的正半轴相交，当直线在两坐标轴上的截距之和最小时，求此直线方程．
在平面直角坐标系中，设点P（X，Y）定义[OP]=|x|+|y|，其中O为坐标原点，对于以下结论：①符合[OP]=1的点P的轨迹围成的图形的面积为2；
②设P为直线
5
x+2y-2=0上任意一点，则[OP]的最小值为1；
③设P为直线y=kx+b（k，b∈R）上的任意一点，则“使[OP]最小的点P有无数个”的必要不充分条件是“k=±1”；其中正确的结论有______（填上你认为正确的所有结论的序号）
求a的值，使直线l1：（a+2）x+（1-a）y-1=0与直线l2：（a-1）x+（2a+3）y+2=0互相垂直．
直线ax+4y-3=0与直线x+ay+5=0平行，则实数a的值为______．
有下列三条直线：①l1：
x
2
+
y
4
=1；②l2：x+y+4=0；③l3：y+4=-3（x-2）．
其中与直线y=2x-4在y轴上的截距相等的有______．（只需填写序号）
已知点P（b，a），直线
x
a
+
y
b
=1(a≠b)与x轴、y轴分别交于A、B两点．设直线PA、PB、AB的斜率分别为k1、k2、k3．
（1）当a=2，b=1时，求k1k2k3的值；
（2）求证：不论a，b为何实数，k1k2k3的值都为定值．
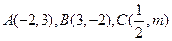若三点共线 则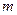的值为（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网