题目内容
已知椭圆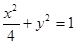 的焦点为
的焦点为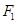 ,
,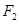 ,在长轴
,在长轴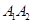 上任取一点
上任取一点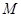 ,过
,过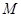 作垂直于
作垂直于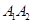 的直线交椭圆于点
的直线交椭圆于点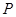 ,则使得
,则使得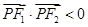 的点
的点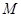 的概率为( )
的概率为( )
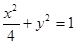 的焦点为
的焦点为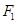 ,
,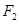 ,在长轴
,在长轴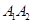 上任取一点
上任取一点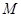 ,过
,过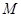 作垂直于
作垂直于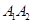 的直线交椭圆于点
的直线交椭圆于点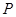 ,则使得
,则使得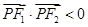 的点
的点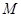 的概率为( )
的概率为( )A.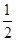 | B.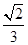 | C. | D.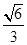 |
D
试题分析:设
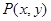 ,则
,则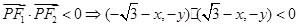
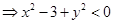 ,
,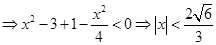 ,概率为
,概率为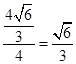 ,选D
,选D点评:求几何概率的基本题型有:长度问题、角度问题、面积问题、体积问题与及生活中实际问题(如时间)等等.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
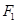 ,
,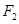 是椭圆
是椭圆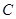 的两个焦点,焦距为4.若
的两个焦点,焦距为4.若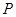 为椭圆
为椭圆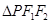 的周长为14,则椭圆
的周长为14,则椭圆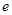 为______________
为______________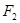 作垂直于实轴的弦
作垂直于实轴的弦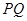 ,
,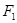 是另一焦点,若∠
是另一焦点,若∠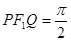 ,则双曲线的离心率
,则双曲线的离心率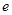 等于( )
等于( )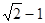


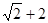
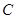 :
: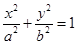
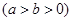 的离心率为
的离心率为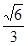 ,过右焦点
,过右焦点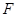 且斜率为
且斜率为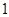 的直线交椭圆
的直线交椭圆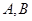 两点,
两点,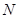 为弦
为弦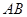 的中点,
的中点,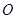 为坐标原点.
为坐标原点.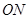 的斜率
的斜率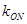 ;
;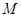 ,都存在
,都存在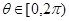 ,使得
,使得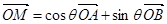 成立.
成立.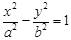 (a>0,b>0) 的左、右焦点,过F1的直线与
(a>0,b>0) 的左、右焦点,过F1的直线与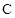 的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3 : 4 : 5,则双 曲线的离心率为 .
的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3 : 4 : 5,则双 曲线的离心率为 .
 左、右焦点分别为F1、F2,焦距为4,点M是椭圆C上一点,满足
左、右焦点分别为F1、F2,焦距为4,点M是椭圆C上一点,满足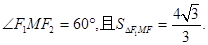
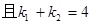 ,求证:直线AB过定点,并求出直线AB的斜率k的取值范围。
,求证:直线AB过定点,并求出直线AB的斜率k的取值范围。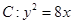 的焦点为
的焦点为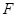 ,准线与
,准线与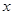 轴的交点为
轴的交点为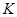 ,点
,点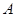 在
在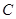 上且
上且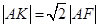 ,则
,则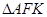 的面积为
的面积为 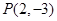 是双曲线
是双曲线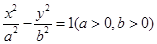 上一点,双曲线两个焦点间的距离等于4,则该双曲线方程是___________.
上一点,双曲线两个焦点间的距离等于4,则该双曲线方程是___________.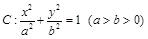 的左、右焦点分别为
的左、右焦点分别为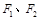 ,上顶点为
,上顶点为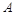 ,离心率为
,离心率为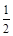 , 在
, 在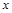 轴负半轴上有一点
轴负半轴上有一点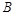 ,且
,且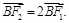
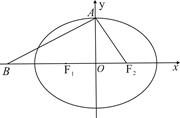
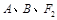 三点的圆 恰好与直线
三点的圆 恰好与直线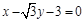 相切,求椭圆C的方程;
相切,求椭圆C的方程;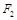 作斜率为
作斜率为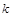 的直线
的直线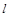 与椭圆C交于
与椭圆C交于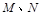 两点,在
两点,在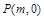 ,使得以
,使得以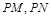 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出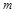 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.