题目内容
【题目】设数列![]() ,
,![]() ,
,![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,![]() ,
,![]() ,且对任意的
,且对任意的![]() 都有
都有![]() ,已知
,已知![]() ,数列
,数列![]() 和
和![]() 是公差不为0的等差数列,且各项均为非负整数.
是公差不为0的等差数列,且各项均为非负整数.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)若数列![]() 的前4项删去1项后按原来顺序成等比数列,求所有满足条件的数列
的前4项删去1项后按原来顺序成等比数列,求所有满足条件的数列![]() ;
;
(3)若![]() ,且
,且![]() ,
,![]() ,求数列
,求数列![]() ,
,![]() 的通项公式.
的通项公式.
【答案】(1)见解析(2)![]() 或
或![]() 或
或![]() .(3)
.(3)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据![]() 得
得![]() 作差即可得证;
作差即可得证;
(2)分类讨论删除的项,分析等比数列的通项公式;
(3)求出![]() ,根据
,根据![]() ,所以
,所以![]() ,转化为不等式恒成立求参数,即可得解.
,转化为不等式恒成立求参数,即可得解.
解:(1)因为![]() ,①
,①
所以![]() ,②
,②
②-①得![]() ,
,
即![]() ,③
,③
所以![]() .④
.④
④-③得![]() ,即
,即![]()
因为![]() ,所以数列
,所以数列![]() 是等差数列.
是等差数列.
(2)在![]() 中,令
中,令![]() 得
得![]() ,
,
设数列![]() 的公差为
的公差为![]() ,则
,则![]() ,
,
因为数列![]() 的前4项
的前4项![]() ,
,![]() ,
,![]() ,
,![]() 删去1项后成等比数列,所以有
删去1项后成等比数列,所以有
①若删去![]() 或
或![]() ,剩下的三项连续,若成等比数列,则
,剩下的三项连续,若成等比数列,则![]() ,则数列
,则数列![]() 的通项公式为
的通项公式为![]() ;
;
②若删去![]() ,即
,即![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,解得
,解得![]() 或
或![]() ,则数列
,则数列![]() 的通项公式为
的通项公式为![]() 或
或![]() ;
;
③若删去![]() ,即
,即![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,解得
,解得![]() 或
或![]() ,则数列
,则数列![]() 的通项公式为
的通项公式为![]() 或
或![]() .
.
综上所述,满足条件的数列![]() 有
有![]() 或
或![]() 或
或![]() .
.
(3)![]() ,则
,则![]() ,
,![]() .
.
因为对任意的![]() 都有
都有![]() ,所以对任意的
,所以对任意的![]() 都有
都有![]() .
.
设数列![]() ,
,![]() 的公差分别为
的公差分别为![]() ,
,![]() ,则
,则
![]() ,
,![]() ,
,
所以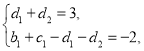 即
即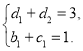 ①
①
因为对任意的![]() 都有
都有![]() ,
,
所以![]() ,
,
整理得![]() ,
,![]() ,
,
所以![]() ,且由
,且由![]() 可得
可得![]() ,②
,②
因为数列![]() ,
,![]() 的各项均为非负整数,
的各项均为非负整数,
所以由②得![]() ,
,![]() .③
.③
由①③得![]() 且
且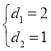 ,
,
故![]() ,
,![]() ,
,![]() .
.

【题目】“共享单车”的出现,为我们提供了一种新型的交通方式。某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:

(1)根据茎叶图,比较两城市满意度评分的平均值的大小及方差的大小(不要求计算出具体值,给出结论即可);
(2)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此2×2列联表,并据此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关;
A | B | 合计 | |
认可 | |||
不认可 | |||
合计 |
(3)在A,B城市对此种交通方式“认可”的用户中按照分层抽样的方法抽取6人,若在此6人中推荐2人参加“单车维护”志愿活动,求A城市中至少有1人的概率。
参考数据如下:(下面临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式 ,其中
,其中![]() )
)