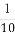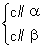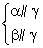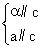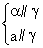题目内容
设S为复数集C的非空子集.若对任意x,y∈S,都有x+y,x-y,xy∈S,则称S为封闭集.下列命题:
①集合S={a+bi|a,b为整数,i为虚数单位}为封闭集;
②若S为封闭集,则一定有0∈S;
③封闭集一定是无限集;
④若S为封闭集,则满足S⊆T⊆C的任意集合T也是封闭集.
其中真命题有 (写出所有真命题的序号).
①②
【解析】设x=a1+b1i,y=a2+b2i,a1,b1,a2,b2为整数,
则x+y=(a1+a2)+(b1+b2)i,x-y=(a1-a2)+(b1-b2)i,xy=(a1a2-b1b2)+(a1b2+a2b1)i,
由于a1,b1,a2,b2为整数,
故a1±a2,b1±b2,a1a2-b1b2,a1b2+a2b1都是整数,
所以x+y,x-y,xy∈S,
故集合S={a+bi|a,b为整数,i为虚数单位}为封闭集,①是真命题;若S是封闭集,且x=y∈S,则根据封闭集的定义,x-y=x-x=0∈S,故命题②正确;集合S={0},显然是封闭集,故封闭集不一定是无限集,命题③不正确;集合S={0}⊆{0,1}=T⊆C,容易验证集合T不是封闭集,故命题④不是真命题.
【方法技巧】集合新定义问题的解题技巧
这种新定义的题目关键就是抓住新定义的本质,紧扣新定义进行推理论证,本题中就是根据封闭集满足其集合中的任意两个元素的和、差、积还是这个集合中的元素.判断一个元素是不是集合中的元素,就看这个元素是否符合集合中代表元素的特征.

练习册系列答案
相关题目