题目内容
的展开式中各项系数和是512，则展开式中常数项是 ．
【答案】分析：观察
可知，展开式中各项系数的和为512，即Cn+Cn1+Cn2++Cnn=512，从而得n，利用二项展开式中的第r+1项，即通项公式Tr+1=cnr（ 
）n-r（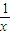 
）r，将n代入，并整理，令x的次数为0，解出r，从而得解．
解答：解：由题意得Cn+Cn1+Cn2++Cnn=512，
即2n=512，解得n=9．该二项展开式中的第r+1项为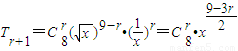
令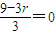
，得r=3，此时，常数项为T4=C93=84．
故答案为：84．
点评：本题主要考查了二项式定理的应用，课本中的典型题目，套用公式解题时，易出现计算错误，二项式的考题难度相对较小，注意三基训练．
可知，展开式中各项系数的和为512，即Cn+Cn1+Cn2++Cnn=512，从而得n，利用二项展开式中的第r+1项，即通项公式Tr+1=cnr（ ）n-r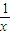（ ）r，将n代入，并整理，令x的次数为0，解出r，从而得解．解答：解：由题意得Cn+Cn1+Cn2++Cnn=512，
即2n=512，解得n=9．该二项展开式中的第r+1项为
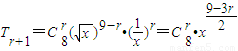
令
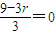，得r=3，此时，常数项为T4=C93=84．故答案为：84．
点评：本题主要考查了二项式定理的应用，课本中的典型题目，套用公式解题时，易出现计算错误，二项式的考题难度相对较小，注意三基训练．
练习册系列答案
相关题目