题目内容
3.有两直线ax-2y-2a+4=0和2x-(1-a2)y-2-2a2=0,当a在区间(0,2)内变化时,求直线与两坐标轴围成的四边形面积的最小值.分析 利用直线方程,求出相关点的坐标,利用直线系解得yE=2.根据S四边形OCEA=S△BCE-S△OAB即可得出.
解答 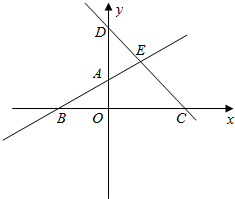 解:∵0<a<2,
解:∵0<a<2,
可得l1:ax-2y=2a-4,与坐标轴的交点A(0,-a+2),B(2-$\frac{4}{a}$,0).
l2:2x-(1-a2)y-2-2a2=0,与坐标轴的交点C(a2+1,0),D(0,$\frac{-2-2{a}^{2}}{1-{a}^{2}}$).
两直线ax-2y-2a+4=0和2x-(1-a2)y-2-2a2=0,都经过定点(2,2),即yE=2.
∴S四边形OCEA=S△BCE-S△OAB
=$\frac{1}{2}$|BC|•yE-$\frac{1}{2}$|OA|•|OB|
=$\frac{1}{2}$(a2+$\frac{4}{a}$-1)×2-$\frac{1}{2}$(2-a)×($\frac{4}{a}$-2)
=a2-a+3
=(a-$\frac{1}{2}$)2+$\frac{11}{4}$≥$\frac{11}{4}$,当a=$\frac{1}{2}$时取等号.
∴l1,l2与坐标轴围成的四边形面积的最小值为$\frac{11}{4}$.
点评 本题考查了相交直线、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
5.设函数y=$\frac{1}{\sqrt{{x}^{2}-3x-10}}$的定义域为A,B={x||x-m|<6},且A∪B=R,则实数m的取值范围是( )
| A. | -1<m<4 | B. | -1<m<3 | C. | 1<m<4 | D. | 1<m<3 |
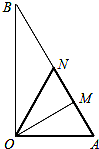 如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边A,B上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.
如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边A,B上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.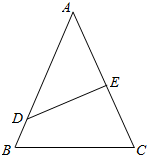 某校把一块形状为正三角形的边角地ABC开辟为生态园,如图所示,其中AB=2a,DE把三角形分成面积相等的两个部分,D在线段AB上,E在线段AC上.
某校把一块形状为正三角形的边角地ABC开辟为生态园,如图所示,其中AB=2a,DE把三角形分成面积相等的两个部分,D在线段AB上,E在线段AC上.