题目内容
(本小题满分12分)
已知函数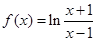
(1)求函数的定义域,并证明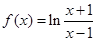 在定义域上是奇函数;
在定义域上是奇函数;
(2)对于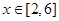
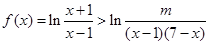 恒成立,求实数
恒成立,求实数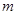 的取值范围;
的取值范围;
已知函数
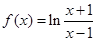
(1)求函数的定义域,并证明
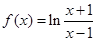 在定义域上是奇函数;
在定义域上是奇函数;(2)对于
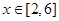
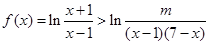 恒成立,求实数
恒成立,求实数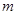 的取值范围;
的取值范围;解:(1)由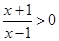 ,解得
,解得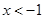 或
或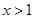 ,
,
∴ 函数的定义域为 ………2分
………2分
当 时,
时,
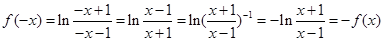
∴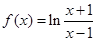 在定义域上是奇函数。 ………….5分
在定义域上是奇函数。 ………….5分
(2)由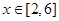 时,
时,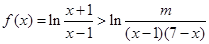 恒成立,
恒成立,
∴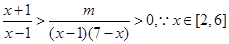 …………………7分
…………………7分
∴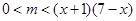 在
在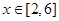 成立 …………………8分
成立 …………………8分
令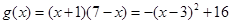 ,
,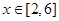 ,由二次函数的性质可知
,由二次函数的性质可知
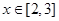 时函数单调递增,
时函数单调递增,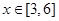 时函数单调递减,
时函数单调递减,
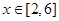 时,
时,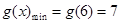 …………….11分
…………….11分
∴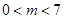 ……………….12分
……………….12分
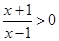 ,解得
,解得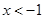 或
或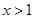 ,
,∴ 函数的定义域为
 ………2分
………2分当
 时,
时,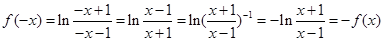
∴
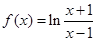 在定义域上是奇函数。 ………….5分
在定义域上是奇函数。 ………….5分(2)由
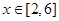 时,
时,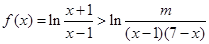 恒成立,
恒成立,∴
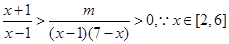 …………………7分
…………………7分∴
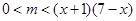 在
在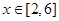 成立 …………………8分
成立 …………………8分令
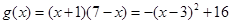 ,
,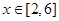 ,由二次函数的性质可知
,由二次函数的性质可知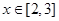 时函数单调递增,
时函数单调递增,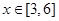 时函数单调递减,
时函数单调递减,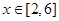 时,
时,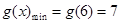 …………….11分
…………….11分∴
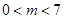 ……………….12分
……………….12分略

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
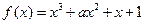 ,(
,(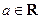 )
)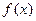 的单调区间;
的单调区间;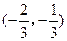 内是减函数,求
内是减函数,求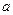 的取值范围.
的取值范围.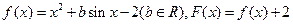 ,且对于任意实数
,且对于任意实数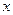 ,恒有
,恒有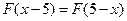 。
。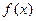 的解析式;
的解析式;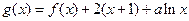 在区间
在区间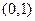 上单调,求实数
上单调,求实数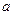 的取值范围;
的取值范围;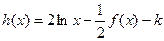 有几个零点?
有几个零点?
 的单调性;
的单调性; 的最大值和最小值.
的最大值和最小值.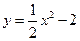 在点
在点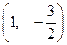 处切线的倾斜角为 ( )
处切线的倾斜角为 ( )
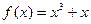 在点
在点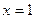 处的切线方程为 ( )
处的切线方程为 ( )



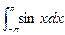 的值为( )
的值为( )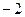
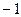
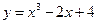 在点
在点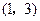 处的切线的倾斜角为
处的切线的倾斜角为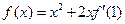 ,若
,若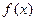 在R上可导,则
在R上可导,则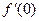 = ,
= ,