题目内容
设数列{2n-1}按第n组有n个数(n是正整数)的规则分组如下:(1),(2,4),(8,16,32),…,则第101组中的第一个数为( )
| A.24 951 |
| B.24 950 |
| C.25 051 |
| D.25 050 |
D
本试题主要是考学生灵活运用等比、等差数列的前n项和的公式及等比数列的通项公式化简求值,是一道中档题。
因为第一组数一个数,第二组数有2个,依次可知,第100组有100个数,则可知100组的最后一个数即为以1为首项,公比为2的等比数列的前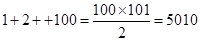 ,则第101组中的第一个数为25 050,选D.
,则第101组中的第一个数为25 050,选D.
解决该试题的关键是根据数列{2n-1}按“第n组有n个数(n∈N+)”的规则分组,可知第101组中的第一个数前面有1+2+..+100个数,利用等差数列的前n项和的公式求出数的个数,又因为数列{2n-1}以1为首项,2为公比的等比数列,写出此等比数列的通项公式,把求出的个数加1代入通项公式中即可得到第101组中的第一个数。
因为第一组数一个数,第二组数有2个,依次可知,第100组有100个数,则可知100组的最后一个数即为以1为首项,公比为2的等比数列的前
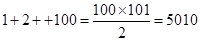 ,则第101组中的第一个数为25 050,选D.
,则第101组中的第一个数为25 050,选D.解决该试题的关键是根据数列{2n-1}按“第n组有n个数(n∈N+)”的规则分组,可知第101组中的第一个数前面有1+2+..+100个数,利用等差数列的前n项和的公式求出数的个数,又因为数列{2n-1}以1为首项,2为公比的等比数列,写出此等比数列的通项公式,把求出的个数加1代入通项公式中即可得到第101组中的第一个数。

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
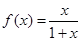
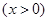 ,数列
,数列 满足:
满足: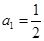 ,
,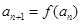
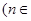 N*
N*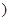 .
.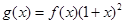 ,数列
,数列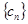 满足:
满足: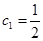 ,
,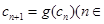 N*),
N*), 的正整数,都满足:
的正整数,都满足: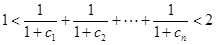 .
.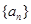 中,前
中,前 项和
项和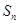 ,且
,且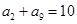 ,则
,则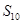 等于( )
等于( )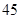



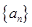 满足
满足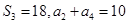 。
。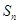 的最大值;
的最大值;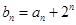 ,求数列
,求数列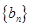 的其前
的其前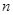 项和
项和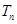 .
.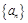 中,若
中,若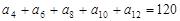 ,则
,则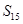 的值为: ( )
的值为: ( )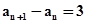 ,则数列
,则数列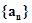 是( )
是( )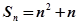 ,那么它的通项公式为an="_________" .
,那么它的通项公式为an="_________" .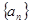 中,
中,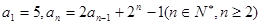 ,若存在实数
,若存在实数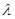 ,使得数列
,使得数列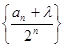 为等差数列,则
为等差数列,则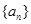 中,
中,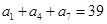 ,
,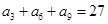 ,则数列
,则数列