题目内容
(理)已知点 是圆
是圆 上的动点.
上的动点.
(1)求点 到直线
到直线 的距离的最小值;
的距离的最小值;
(2)若直线 与圆
与圆 相切,且
相切,且 与x,y轴的正半轴分别相交于
与x,y轴的正半轴分别相交于 两点,求
两点,求 的面积最小时直线
的面积最小时直线 的方程;
的方程;
 是圆
是圆 上的动点.
上的动点.(1)求点
 到直线
到直线 的距离的最小值;
的距离的最小值;(2)若直线
 与圆
与圆 相切,且
相切,且 与x,y轴的正半轴分别相交于
与x,y轴的正半轴分别相交于 两点,求
两点,求 的面积最小时直线
的面积最小时直线 的方程;
的方程;(1)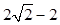 (2)
(2)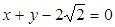
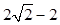 (2)
(2)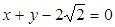
试题分析:解:(1)圆心到直线l的距离为
 , 所以P到直线l:
, 所以P到直线l: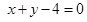 的距离的最小值为:
的距离的最小值为: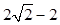
(2)设直线l的方程为:
 ,因为l与x,y轴的正半轴分别相交于A,B两点,则
,因为l与x,y轴的正半轴分别相交于A,B两点,则 ,
,且
 ,又l与圆C相切,则C点到直线l的距离等于圆的半径2,
,又l与圆C相切,则C点到直线l的距离等于圆的半径2,即:
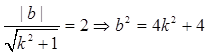 , ①,
, ①,而
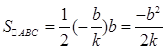 ②
② 将①代入②得
 ,
,当且仅当
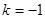 时取等号,所以当
时取等号,所以当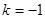 时,
时,  的面积最小,此时
的面积最小,此时 ,直线l的方程为:
,直线l的方程为: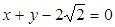
点评:解决该试题中圆上点到直线的距离的最值问题,直接转化为圆心到直线的距离加上圆的半径为最大值,减去圆的半径为最小值得到。这是高考中常考的一个知识点,要熟练的掌握。

练习册系列答案
相关题目
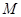 过两点
过两点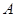 (1,-1),
(1,-1),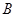 (-1,1),且圆心
(-1,1),且圆心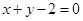 上.
上.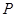 是直线
是直线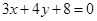 上的动点,
上的动点,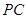 、
、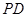 是圆
是圆 、
、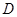 为切点,求四边形
为切点,求四边形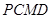 面积的最小值.
面积的最小值. 轴上,且过两点
轴上,且过两点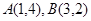 的圆的方程为 .
的圆的方程为 .  与圆C2:
与圆C2: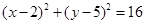 的位置关系是( )
的位置关系是( ) 表示一个圆,则有( )
表示一个圆,则有( )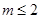
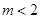
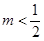

 的点数共有 个。
的点数共有 个。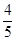 |PD|.
|PD|.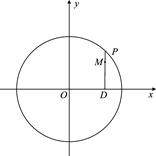
 :x+y+1=0的距离为
:x+y+1=0的距离为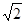 的点共有( )
的点共有( )