题目内容
双曲线 =1和椭圆
=1和椭圆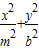 =1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )
=1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )A.锐角三角形
B.钝角三角形
C.直角三角形
D.等腰三角形
【答案】分析:求出椭圆与双曲线的离心率,利用离心率互为倒数,推出a,b,m的关系,判断三角形的形状.
解答:解:双曲线 =1和椭圆
=1和椭圆 =1(a>0,m>b>0)的离心率互为倒数,所以
=1(a>0,m>b>0)的离心率互为倒数,所以 ,
,
所以b2m2-a2b2-b4=0即m2=a2+b2,所以以a,b,m为边长的三角形是直角三角形.
故选C.
点评:本题是中档题,考查椭圆与双曲线基本性质的应用,三角形形状的判断方法,考查计算能力.
解答:解:双曲线
 =1和椭圆
=1和椭圆 =1(a>0,m>b>0)的离心率互为倒数,所以
=1(a>0,m>b>0)的离心率互为倒数,所以 ,
,所以b2m2-a2b2-b4=0即m2=a2+b2,所以以a,b,m为边长的三角形是直角三角形.
故选C.
点评:本题是中档题,考查椭圆与双曲线基本性质的应用,三角形形状的判断方法,考查计算能力.

练习册系列答案
相关题目
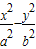 =1和椭圆
=1和椭圆 =1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )
=1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( ) =1和椭圆
=1和椭圆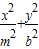 =1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )
=1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( ) =1和椭圆
=1和椭圆 =1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )
=1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )