题目内容
(本小题12分)已知数列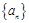 是各项均不为
是各项均不为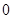 的等差数列,公差为
的等差数列,公差为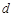 ,
,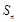 为其前
为其前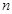 项和,且满足
项和,且满足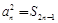 ,
,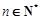 .数列
.数列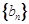 满足
满足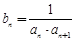 ,
,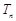 为数列
为数列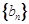 的前n项和.
的前n项和.
(Ⅰ)求数列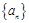 的通项公式
的通项公式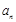 和数列
和数列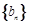 的前n项和
的前n项和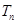 ;
;
(Ⅱ)若对任意的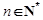 ,不等式
,不等式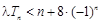 恒成立,求实数
恒成立,求实数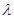 的取值范围;
的取值范围;
【答案】
(1)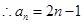 ,
,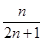 (2)
(2)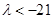
【解析】
试题分析:解(1)在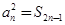 中,令
中,令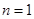 ,
,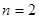 ,
,
得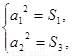 即
即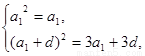
解得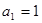 ,
,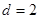 ,
,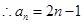
又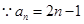 时,
时,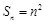 满足
满足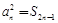 ,
,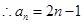 ………………3分
………………3分
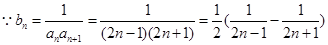 ,
,
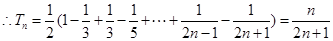 . ………………6分
. ………………6分
(2)①当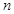 为偶数时,要使不等式
为偶数时,要使不等式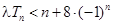 恒成立,即需不等式
恒成立,即需不等式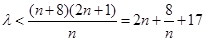 恒成立.
恒成立.
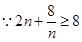 ,等号在
,等号在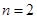 时取得.
时取得.
 此时
此时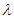 需满足
需满足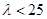 . …………………………………………8分
. …………………………………………8分
②当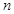 为奇数时,要使不等式
为奇数时,要使不等式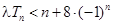 恒成立,即需不等式
恒成立,即需不等式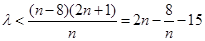 恒成立.
恒成立.
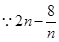 是随
是随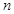 的增大而增大,
的增大而增大, 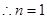 时
时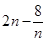 取得最小值
取得最小值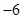 .
.
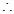 此时
此时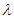 需满足
需满足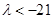 . …………………………………………11分
. …………………………………………11分
综合①、②可得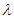 的取值范围是
的取值范围是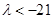 . ………………………………………12分
. ………………………………………12分
考点:本试题考查了数列的通项公式和数列求和求解。
点评:对于等差数列求解通项公式,主要求解两个基本元素,首项和公差即可。同时对于数列的求和中裂项求和要给予关注,高考常考查,而对于数列与不等式恒成立结合的问题,通常情况下,采用分离的思想来得到范围,属于难度试题。

练习册系列答案
相关题目
 中,
中, 。
。 中,
中, ,求数列
,求数列 项和
项和 .
. 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程 ;
; 过
过 且与圆C相切,求直线
且与圆C相切,求直线 ,使直线
,使直线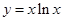
 处的切线方程。
处的切线方程。