题目内容
在△ABC中，B＝60°，AC＝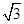
，则AB＋2BC的最大值为________．
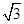，则AB＋2BC的最大值为________．2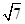
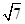
A＋C＝120°⇒C＝120°－A，A∈(0°，120°)，
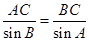＝2⇒BC＝2sin A，
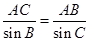＝2⇒AB＝2sin C＝2sin(120°－A)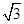＝cos A＋sin A，
∴AB＋2BC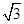＝cos A＋5sin A＝
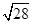sin(A＋φ)＝2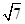sin(A＋φ)，其中tan φ＝
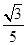，故最大值是2.
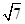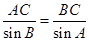＝2⇒BC＝2sin A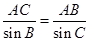，＝2⇒AB＝2sin C＝2sin(120°－A)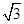＝cos A＋sin A，∴AB＋2BC＝
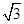cos A＋5sin A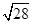＝sin(A＋φ)＝2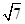sin(A＋φ)，其中tan φ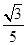＝，故最大值是2.
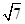练习册系列答案
全能闯关100分系列答案
相关题目
中，
分别是角Ａ，Ｂ，Ｃ的对边，且满足
．
，且
，求最小边长．
＝0
＝0
中，
，
，
，则
.
的值域是 .
，在
上取一点P，使
,求
中，已知点
在
边上，
,
, 
,则
的长为 .
，则cos2
＝( )
