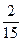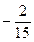题目内容
已知直线l1的方程为3x+4y-12=0,求满足下列条件的直线l2的方程.
(1)l1与l2平行且过点(-1,3)
(2)l1与l2垂直且与两坐标轴围成的三角形面积为4.
(1)l1与l2平行且过点(-1,3)
(2)l1与l2垂直且与两坐标轴围成的三角形面积为4.
(1)直线l1:3x+4y-12=0,k1=-
,
∵l1∥l2∴k2=k1=-
,
∴直线l2:y=-
(x+1)+3,
即3x+4y-9=0,
(2)∵l1⊥l2,
∴k2=
,
设l2的方程为y=
x+b,
则它与两坐标轴交点是(0,b),(-
b,0),
∴S=
|b|•|-
b|=4,即b2=
,
∴b=±
,
∴直线l2的方程是y=
x±
.
| 3 |
| 4 |
∵l1∥l2∴k2=k1=-
| 3 |
| 4 |
∴直线l2:y=-
| 3 |
| 4 |
即3x+4y-9=0,
(2)∵l1⊥l2,
∴k2=
| 4 |
| 3 |
设l2的方程为y=
| 4 |
| 3 |
则它与两坐标轴交点是(0,b),(-
| 3 |
| 4 |
∴S=
| 1 |
| 2 |
| 3 |
| 4 |
| 32 |
| 3 |
∴b=±
4
| ||
| 3 |
∴直线l2的方程是y=
| 4 |
| 3 |
4
| ||
| 3 |

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 ,则直线
,则直线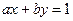 恒过定点 .
恒过定点 .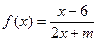 的图象关于直线
的图象关于直线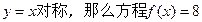 的解为( )
的解为( )