题目内容
16.f(x)是定义域为R的偶函数,f′(x)为f(x)的导函数,当x≤0时,恒有f(x)+xf′(x)<0,设g(x)=xf(x),则满足g(2x-1)<g(3)的实数x的取值范围是( )| A. | (2,+∞) | B. | (-1,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,2) |
分析 根据已知条件利用函数的单调性和奇偶性构造出新函数,利用xf′(x)+f(x)<0,得到:[xf(x)]′<0,进一步分析出偶函数的单调性在对称区间内单调性相反.故建立不等式,解出即可.
解答 解:定义在R上的偶函数f(x),
所以:f(-x)=f(x)
由f(x)的导函数为f′(x),
当x∈(-∞,0]时,恒有xf′(x)+f(x)<0
即:[xf(x)]′<0
所以:函数F(x)=xf(x)在(-∞,0)上是单调递减函数.
由于f(x)为偶函数,
令g(x)=xf(x),
则:g(x)为奇函数.
所以函数g(x)=xf(x)在(0,+∞)上是单调递减函数.
则:满足g(3)>g(2x-1)满足的条件是:2x-1<3,解得:x<2,
所以x的范围是:(-∞,2)
故选:D.
点评 本题考查的知识要点:函数的性质的应用,单调性和奇偶性的应用,构造性函数解不等式组.属于中档题.

练习册系列答案
相关题目
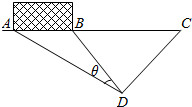 如图所示,足球门左右门柱分别立在A、B处,假定足球门宽度AB为7米,在距离右门柱15米的C处,一球员带球沿与球门线AC成28°角的CD方向以平均每秒6.5米的速度推进,2秒后到达D处射门.问:
如图所示,足球门左右门柱分别立在A、B处,假定足球门宽度AB为7米,在距离右门柱15米的C处,一球员带球沿与球门线AC成28°角的CD方向以平均每秒6.5米的速度推进,2秒后到达D处射门.问: