题目内容
已知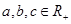 ,且
,且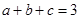 ,
,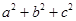 的最小值为
的最小值为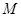 .
.
(1)求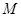 的值;
的值;
(2)解关于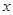 的不等式
的不等式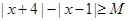 .
.
(1)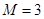 ;(2)
;(2)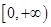 .
.
解析试题分析:本小题主要考查利用柯西不等式求最值、绝对值不等式的解法等基础知识;考查运算求解能力;化归与转化、分类与整合的思想.第一问,利用柯西不等式求最小值,注意等号成立的条件;第二问,利用第一问的结论,用零点分段法去掉绝对值,解不等式.
试题解析:(1)根据柯西不等式,有: , 1分
, 1分
∴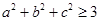 ,当且仅当
,当且仅当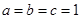 时等号成立. 2分
时等号成立. 2分
即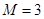 . 3分
. 3分
(2)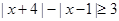 可化为
可化为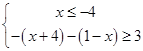 或
或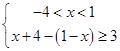 或
或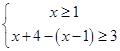 , 5分
, 5分
解得,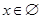 或
或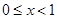 或
或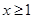 , 6分
, 6分
所以,综上所述,原不等式的解集为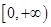 . 7分
. 7分
考点:利用柯西不等式求最值、绝对值不等式的解法.

练习册系列答案
相关题目
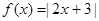 .
.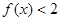 ;
;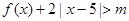 对一切实数
对一切实数 均成立,求
均成立,求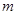 的取值范围.
的取值范围. .
. ;
;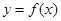 的最小值.
的最小值.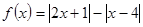 .
.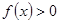 ;
; 对一切实数
对一切实数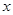 均成立,求
均成立,求 的取值范围.
的取值范围. .
. 的解集A;
的解集A;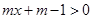 对任何
对任何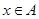 恒成立,求
恒成立,求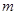 的取值范围.
的取值范围.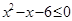 解集为
解集为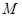 ,不等式
,不等式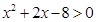 解集为
解集为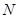 ,不等式
,不等式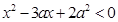
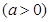 解集为
解集为 .
.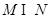 ;
; 的取值范围.
的取值范围.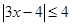 的解集是
的解集是