题目内容
关于函数f(x)=loga
(a>0且a≠1)下列说法:
①f(x)的定义域是(-1,1);
②当a>1时,使f(x)>0的x的取值范围是(-1,0);
③对定义域内的任意x,f(x)满足f(-x)=-f(x);
④当0<a<1时,如果0<x1<x2<1,则f(x1)<f(x2);
其中正确结论的序号是______.(填上你认为正确的所有结论序号)
| 1+x |
| 1-x |
①f(x)的定义域是(-1,1);
②当a>1时,使f(x)>0的x的取值范围是(-1,0);
③对定义域内的任意x,f(x)满足f(-x)=-f(x);
④当0<a<1时,如果0<x1<x2<1,则f(x1)<f(x2);
其中正确结论的序号是______.(填上你认为正确的所有结论序号)
由
>0,得(x+1)(x-1)<0,解得:-1<x<1,∴f(x)的定义域是(-1,1),命题①正确;
∵a>1,由f(x)>0得,
>1,即
-1>0,x(x-1)<0,解得0<x<1,
∴当a>1时,使f(x)>0的x的取值范围是(0,1),命题②不正确;
∵f(-x)=loga
=-loga
=-f(x),∴命题③正确;
当0<a<1时,若0<x1<x2<1,则1-x1x2+x2-x1>1-x1x2+x1-x2>0,
∴f(x1)-f(x2)=loga
-loga
=loga(
•
)=loga
>0.
∴f(x1)>f(x2)命题④不正确.
故答案为:①③.
| 1+x |
| 1-x |
∵a>1,由f(x)>0得,
| 1+x |
| 1-x |
| 1+x |
| 1-x |
∴当a>1时,使f(x)>0的x的取值范围是(0,1),命题②不正确;
∵f(-x)=loga
| 1-x |
| 1+x |
| 1+x |
| 1-x |
当0<a<1时,若0<x1<x2<1,则1-x1x2+x2-x1>1-x1x2+x1-x2>0,
∴f(x1)-f(x2)=loga
| 1+x1 |
| 1-x1 |
| 1+x2 |
| 1-x2 |
=loga(
| 1+x1 |
| 1-x1 |
| 1-x2 |
| 1+x2 |
| 1+x1-x2-x1x2 |
| 1+x2-x1-x1x2 |
∴f(x1)>f(x2)命题④不正确.
故答案为:①③.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
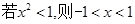 ”的逆否命题是( )
”的逆否命题是( )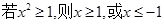
 ,则
,则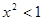
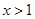 或
或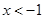 ,则
,则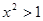
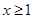 或
或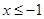 ,则
,则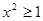
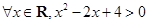 ”的否定为 .
”的否定为 .