题目内容
(本小题10分)
已知函数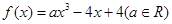 在
在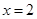
 取得极值。
取得极值。
(Ⅰ)确定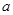 的值并求函数的单调区间;
的值并求函数的单调区间;
(Ⅱ)若关于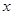 的方程
的方程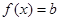 至多有两个零点,
至多有两个零点, 求实数
求实数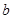 的取值范围。
的取值范围。
【答案】
解(Ⅰ)因为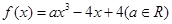 ,
,
所以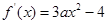
因为函数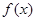 在
在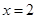 时有极值
时有极值 ,
,
所以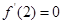 ,即
,即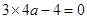
得 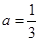 ,
经检验符合题意,所以
,
经检验符合题意,所以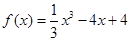
所以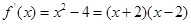
令,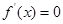 得,
得,
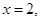 或
或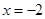
当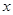 变化时
变化时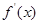 ,
,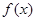 变化如下表:
变化如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
单调递增↗ |
极大值 |
单 |
极小值 |
单调递增↗ |
所以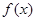 的单调增区间为
的单调增区间为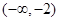 ,
,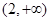 ;
;
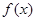 的单调减区间为
的单调减区间为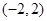 。
。

【解析】略

练习册系列答案
相关题目
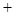

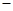
 调递减↘
调递减↘ 当
当 时,求不等式
时,求不等式 的解集;若
的解集;若 的解集包含
的解集包含 ,求a的取值范围。
,求a的取值范围。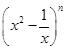 展开式中的二项式系数的和比
展开式中的二项式系数的和比 展开式的二项式系数的和大
展开式的二项式系数的和大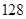 ,求
,求

 且
且 ,求以N(1,1)为圆心,并且与
,求以N(1,1)为圆心,并且与 相切的圆的方程.
相切的圆的方程. 点
点 是
是 的重心,过点
的重心,过点 与
与 分别交于
分别交于 两点.
两点. 表示
表示 ;
; 试问
试问 是否为定值,证明你的结论.
是否为定值,证明你的结论.