题目内容
(本小题10分)已知函数 当
当 时,求不等式
时,求不等式 的解集;若
的解集;若 的解集包含
的解集包含 ,求a的取值范围。
,求a的取值范围。
(1)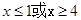 (2)
(2)
解析试题分析::(1)当a=-3时,f(x)≥3 即|x-3|+|x-2|≥3,即x≤2,3-x+2-x≥3,或2<x<3,3-x+x-2≥3或x≥3 x-3+x-2≥3
解得 x≤1或x≥4,故不等式的解集为 {x|x≤1或x≥4}.
(2)原命题即f(x)≤|x-4|在[1,2]上恒成立,等价于|x+a|+2-x≤4-x在[1,2]上恒成立,等价于-2-x≤a≤2-x在[1,2]上恒成立,
解得-3≤a≤0,故a的取值范围为[-3,0].
考点:绝对值不等式的求解
点评:解决的关键是对于分段函数的值域的求解,同时能利用集合的包含关系得到参数的 范围,属于基础题。

练习册系列答案
相关题目
 ,
,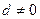 ,
,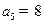 ,且项
,且项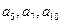 分别是某一等比数列
分别是某一等比数列 中的第
中的第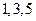 项,(1)求数列
项,(1)求数列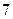 项。
项。
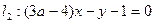 且
且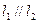 ,求以N(1,1)为圆心,并且与
,求以N(1,1)为圆心,并且与 相切的圆的方程.
相切的圆的方程.
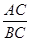 的值.
的值.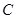 经过
经过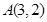 、
、 两点,且圆心在直线
两点,且圆心在直线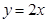 上.
上.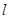 经过点
经过点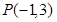 且与圆
且与圆 ,
, ;
; .
.