题目内容
(本小题10分)已知在三棱锥S--ABC中,∠ACB=900,又SA⊥平面ABC,
AD⊥SC于D,求证:AD⊥平面SBC,

【答案】
证明:SA⊥面ABC, BC⊥面ABC,Þ BC ⊥SA;
又BC⊥AC,且AC、SA是面SAC内的两相交线,∴BC⊥面SAC;
又ADÌ面SAC,∴ BC⊥AD,
又已知SC⊥AD,且BC、SC是面SBC内两相交线,∴ AD⊥面SBC。
【解析】略

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ,
,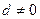 ,
,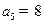 ,且项
,且项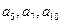 分别是某一等比数列
分别是某一等比数列 中的第
中的第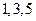 项,(1)求数列
项,(1)求数列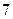 项。
项。
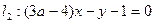 且
且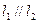 ,求以N(1,1)为圆心,并且与
,求以N(1,1)为圆心,并且与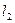 相切的圆的方程.
相切的圆的方程.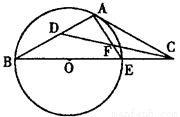
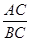 的值.
的值.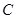 经过
经过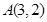 、
、 两点,且圆心在直线
两点,且圆心在直线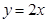 上.
上.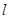 经过点
经过点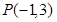 且与圆
且与圆 ,
, ;
; .
.