题目内容
3. 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左、右顶点为A,B,左、右焦点为F1,F2,|AB|=4,|F1F2|=2$\sqrt{3}$.直线y=kx+m(k>0)交椭圆E于C,D两点,与线段F1F2、椭圆短轴分别交于M,N两点(M,N不重合),且|CM|=|DN|.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左、右顶点为A,B,左、右焦点为F1,F2,|AB|=4,|F1F2|=2$\sqrt{3}$.直线y=kx+m(k>0)交椭圆E于C,D两点,与线段F1F2、椭圆短轴分别交于M,N两点(M,N不重合),且|CM|=|DN|.(Ⅰ)求椭圆E的方程;
(Ⅱ)设直线AD,BC的斜率分别为k1,k2,求$\frac{{k}_{1}}{{k}_{2}}$的取值范围.
分析 (Ⅰ)确定2a=4,2c=2$\sqrt{3}$,求出b,即可求椭圆E的方程;
(Ⅱ)直线y=kx+m(k>0)与椭圆联立,利用韦达定理,结合|CM|=|DN|,求出m的范围,再求$\frac{{k}_{1}}{{k}_{2}}$的取值范围.
解答 解:(Ⅰ)因为2a=4,2c=2$\sqrt{3}$,
所以a=2,c=$\sqrt{3}$,
所以b=1,
所以椭圆E的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)直线y=kx+m(k>0)与椭圆联立,可得(4k2+1)x2+x8mk+4m2-4=0.
设D(x1,y1),C(x2,y2),则x1+x2=-$\frac{8mk}{4{k}^{2}+1}$,x1x2=$\frac{4{m}^{2}-4}{4{k}^{2}+1}$,
又M(-$\frac{m}{k}$,0),N(0,m),
由|CM|=|DN|得x1+x2=xM+xN,所以-$\frac{8mk}{4{k}^{2}+1}$=-$\frac{m}{k}$,所以k=$\frac{1}{2}$(k>0).
所以x1+x2=-2m,x1x2=2m2-2.
因为直线y=kx+m(k>0)交椭圆E于C,D两点,与线段F1F2、椭圆短轴分别交于M,N两点(M,N不重合),
所以-$\sqrt{3}$≤-2m≤$\sqrt{3}$且m≠0,
所以($\frac{{k}_{1}}{{k}_{2}}$)2=[$\frac{{y}_{1}({x}_{2}-2)}{{y}_{2}({x}_{1}+2)}$]2=$\frac{(2-{x}_{1})(2-{x}_{2})}{(2+{x}_{2})(2+{x}_{1})}$
=$\frac{4-2({x}_{1}+{x}_{2})+{x}_{1}{x}_{2}}{4+2({x}_{1}+{x}_{2})+{x}_{1}{x}_{2}}$=$\frac{4-2•(-2m)+2{m}^{2}-2}{4+2•(-2m)+2{m}^{2}-2}$=$\frac{(m+1)^{2}}{(m-1)^{2}}$,
所以$\frac{{k}_{1}}{{k}_{2}}$=$\frac{1+m}{1-m}$=-1-$\frac{2}{m-1}$∈[-2$\sqrt{3}$-3,2$\sqrt{3}$-3].
点评 本题考查椭圆的方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,有难度.

| A. | c<a<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |
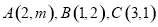 ,若
,若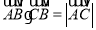 ,则实数
,则实数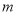 等于( )
等于( )

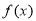 为奇函数,且当
为奇函数,且当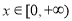 时,
时,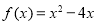 ,则
,则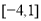 上的最大值为( )
上的最大值为( )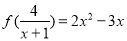 ,则
,则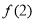 等于( )
等于( )