题目内容
【题目】如图,在多面体![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为菱形,四边形
为菱形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() ,
,![]() ,M为线段
,M为线段![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 将多面体
将多面体![]() 分成的两个部分的体积之比.
分成的两个部分的体积之比.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)延长![]() 交
交![]() 于点G,连接
于点G,连接![]() ,易证
,易证![]() ,可得
,可得![]() ,
,
可得四边形![]() 为平行四边形,可得
为平行四边形,可得![]() ,
,![]() 平面
平面![]() ;
;
(2)分别计算出三棱柱![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积,可得体积之比.
的体积,可得体积之比.
证明:延长![]() 交
交![]() 于点G,连接
于点G,连接![]() ,
,
 .
.
由![]() ,M为
,M为![]() 中点,易证
中点,易证![]() ,
,
所以![]() .
.
因为![]() ,所以
,所以![]() .
.
由已知![]() ,且
,且![]() ,又
,又![]() ,
,
所以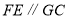 ,且
,且![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
因![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解:由(1)可得,多面体![]() 被平面分成的两个部分是三棱锥
被平面分成的两个部分是三棱锥![]() 和三棱柱
和三棱柱![]() .
.
因为![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() .
.
又易得![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() 即为三棱柱
即为三棱柱![]() 的高.
的高.
所以三棱柱![]() 的体积
的体积![]() ,
,
又易得三棱锥![]() 的体积
的体积![]() ,
,
所以多面体![]() 被分成的两个部分体积比为
被分成的两个部分体积比为![]() .
.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(1)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(2)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励.现用样本估计总体,从上述5个销售单价中任选2个销售单价,下个月分别在两个不同的网店进行销售,求这两个网店下个月获得奖励的总额![]() 的分布列及其数学期望.
的分布列及其数学期望.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为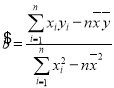 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.