题目内容
已知数列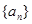 为等比数列,
为等比数列, ,
,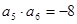 ,则
,则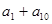 的值为( )
的值为( )
A.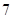 | B.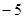 | C. | D.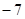 |
D
解析试题分析:因为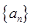 为等比数列,所以
为等比数列,所以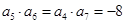 ,又
,又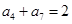 ,所以
,所以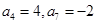 或
或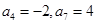 .当
.当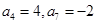 时,
时, ,所以
,所以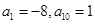 ,所以
,所以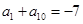 ,同理可求当
,同理可求当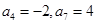 时,
时,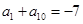 .
.
考点:本小题主要考查等比数列的性质和等比数列中项的计算,考查学生的运算求解能力.
点评:等比数列中任何一项和公比都不能为0.

练习册系列答案
相关题目
已知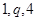 成等比数列,则
成等比数列,则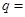 ( )
( )
A.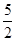 | B.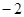 | C.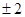 | D.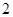 |
两个正数 的等差中项是
的等差中项是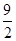 ,一个等比中项是
,一个等比中项是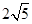 ,且
,且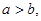 则双曲线
则双曲线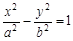 的离心率为( )
的离心率为( )
A. | B.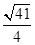 | C.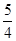 | D.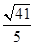 |
已知正项等比数列 满足:
满足: ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D.不存在 |
设 为等比数列
为等比数列 的前
的前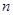 项和,已知
项和,已知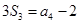 ,
,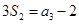 ,则公比
,则公比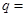 ( )
( )
| A.3 | B.4 | C.5 | D.6 |
等比数列 中,
中,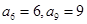 那么
那么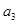 为 ( )
为 ( )
A.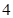 | B.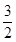 | C.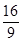 | D.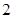 |
在等比数列 中,
中, ,则数列
,则数列 的第4项为
的第4项为
A.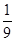 | B.81 | C.-81 | D.81或-81 |
定义在 上的函数
上的函数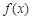 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
,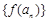 仍是等比数列,则称
仍是等比数列,则称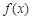 为“保等比数列函数”.现有定义在
为“保等比数列函数”.现有定义在 上的如下函数: ①
上的如下函数: ① ; ②
; ② ; ③
; ③ ; ④
; ④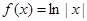 .
.
则其中是“保等比数列函数”的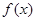 的序号为
的序号为
| A.①② | B.③④ | C.①③ | D.②④ |
各项均为正数的等比数列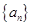 中,
中,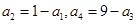 ,则
,则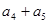 等于( )
等于( )
| A.16 | B.27 | C.36 | D.-27 |