题目内容
2.设抛物线C:y2=2px(p>0)的焦点是F,已知P(2,m)是抛物线C上一点,且|PF|=4.(Ⅰ)求p和m的值;
(Ⅱ)设过点Q(3,2)的直线l1与抛物线C相交于A、B两点,经过点F与直线l1垂直的直线l2交抛物线C于M、N两点,若|MN|是|QA|、|QB|的等比中项,求|MN|.
分析 (Ⅰ)通过将P(2,m)代入抛物线C方程及抛物线的定义计算即得结论;
(Ⅱ)设l1:x=m(y-2)+3(m≠0),l2:x=-$\frac{1}{m}$y+2,A(x1,y1)、B(x2,y2),M(x3,y3)、N(x4,y4),分别与抛物线方程联立,利用韦达定理及|QA|•|QB|=|MN|2,计算即可.
解答 解:(Ⅰ)根据抛物线的定义得|PF|即为点P到准线的距离,
∴|PF|=2+$\frac{p}{2}$=4,∴p=4,
又P(2,m)是抛物线C上一点,
∴m2=2×4×2=16,
∴m=±4;
(Ⅱ)由题可设l1:x=m(y-2)+3(m≠0),
则l2:x=-$\frac{1}{m}$y+2,
由$\left\{\begin{array}{l}{{y}^{2}=8x}\\{x=m(y-2)+3}\end{array}\right.$,得y2-8my+16m-24=0,
设A(x1,y1)、B(x2,y2),
则有y1+y2=8m,y1y2=16m-24,
∴|QA|•|QB|=(1+m2)|y2-2||y1-2|=20(1+m2),
由$\left\{\begin{array}{l}{{y}^{2}=8x}\\{x=-\frac{1}{m}y+2}\end{array}\right.$,得m2y+8y-16m=0,
设M(x3,y3)、N(x4,y4),
则y3+y4=-$\frac{8}{m}$,y3y4=-16,
故|MN|2=(1+$\frac{1}{{m}^{2}}$)|y3-y4|2=$\frac{64(1+{m}^{2})^{2}}{{m}^{4}}$,
由已知20(1+m2)=$\frac{64(1+{m}^{2})^{2}}{{m}^{4}}$,
化简得5m4-16m2-16=0,
解得m2=4,
∴|MN|=10.
点评 本题考查直线与抛物线的位置关系,涉及到韦达定理、等比中项的性质,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案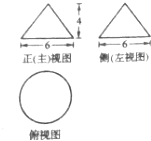 一个圆锥的三视图及其尺寸如图所示,若一个平行于圆锥底面的平面将此圆锥截成体积之比1:7的上、下两部分,则截面的面积为( )
一个圆锥的三视图及其尺寸如图所示,若一个平行于圆锥底面的平面将此圆锥截成体积之比1:7的上、下两部分,则截面的面积为( )| A. | $\frac{π}{3}$ | B. | π | C. | $\frac{9π}{4}$ | D. | 4π |