题目内容
下列命题中,其中正确命题的个数为( )①底面是正多边形的棱锥一定是正棱锥;②所有侧棱长都相等的棱锥一定是正棱锥;③各侧面和底面所成二面角都相等的棱锥一定是正棱锥;④一个棱锥可以有两条侧棱与底面垂直;⑤底面多边形内接于一个圆的棱锥的侧棱长都相等;⑥一个棱锥可以有两个侧面与底面垂直.
A.0 B
答案:B
解析:一个棱锥是正棱锥必须满足两个条件:一是底面是正多边形;二是顶点在底面的射影是底面的中心.由此知①错;②中的条件并没有保证顶点在底面的射影是底面的中心,所以②错.
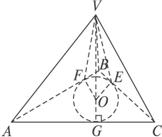
如图,V在底面的射影O为△ABC的内切圆圆心,过O点作OE⊥BC,OF⊥AB,OG⊥AC,连结VE、VF、VG.
∴Rt△VEO≌Rt△VFO≌Rt△VGO.
∴∠VEO=∠VFO=∠VGO.
而∠VEO、∠VFO、∠VGO分别为三棱锥各侧面和底面所成二面角的平面角.
但此三棱锥的顶点V在底面的射影O不一定为底面中心,
∴此三棱锥不一定为正三棱锥.因此③错.
④中若一个棱锥有两条侧棱与底面垂直,则这两条侧棱平行,这是不可能的.
⑤中只有当棱锥的顶点在底面的射影为底面多边形的内接圆的圆心时,利用三角形全等才可得到它的侧棱长都相等.
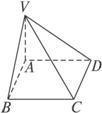
如图所示的四棱锥,VA⊥平面ABCD,则△VAD和△VAB为直角三角形.
所以⑥正确.故选B.

练习册系列答案
相关题目