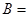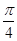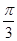题目内容
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.
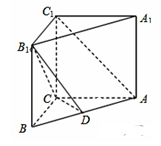
(1)若D是AB中点,求证:AC1∥平面B1CD;
(2)当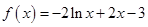 时,求二面角
时,求二面角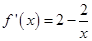 的余弦值.
的余弦值.

(1)若D是AB中点,求证:AC1∥平面B1CD;
(2)当
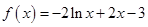 时,求二面角
时,求二面角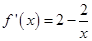 的余弦值.
的余弦值.(1)详见解析;(2)

试题分析:(1)要证明AC1∥平面B1CD,根据线面的判定定理,只要转换证明DE//AC1即可;
(2)可以以C为原点建立空间直角坐标系,求出平面BCD的法向量与平面B1CD的法向量,然后利用向量夹角公式即可.
试题解析:解:(1)证明:连结BC1,交B1C于E,连接DE.
因为直三棱柱ABC-A1B1C1,D是AB中点,

所以侧面BB1C1C为矩形,DE为△ABC1的中位线,所以DE//AC1.
因为DE
 平面B1CD,AC1
平面B1CD,AC1 平面B1CD,所以AC1∥平面B1CD.6分
平面B1CD,所以AC1∥平面B1CD.6分(2)由(1)知AC⊥BC,如图,以C为原点建立空间直角坐标系C-xyz.

则B(3,0,0),A(0,4,0),A1(0,4,4),B1(3,0,4).设D(a,b,0)(
 ,
, ),因为点D在线段AB上,且
),因为点D在线段AB上,且 ,即
,即 .
.所以
 ,
, ,
, ,
, ,
, .
.平面BCD的法向量为
 .设平面B1CD的法向量为
.设平面B1CD的法向量为 ,
,由
 ,
, ,得
,得 ,
,所以
 ,
, ,
, .所以
.所以 .
.所以二面角
 的余弦值为
的余弦值为 .12分
.12分
练习册系列答案
相关题目
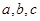 ,且
,且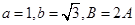 。
。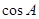 的值;(2)求c的值。
的值;(2)求c的值。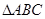 中,内角
中,内角 对边的长分别是
对边的长分别是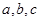 ,且
,且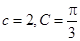 .
. ,求
,求 ;
;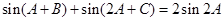 ,求
,求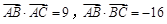 .求:
.求: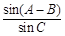 的值.
的值.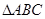 中,
中,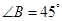 ,
,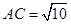 ,
,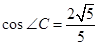 点
点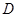 是
是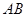 的中点, 求
的中点, 求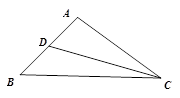
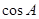 的值和中线
的值和中线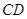 的长
的长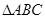 的三个内角满足
的三个内角满足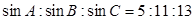 ,则
,则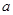 、
、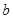 ,若2asinB=
,若2asinB=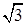 b,则角A等于________.
b,则角A等于________.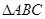 中,
中,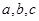 分别是角
分别是角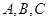 的对边.已知
的对边.已知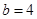 ,
,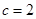 ,
,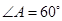 ,则
,则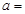 ;
;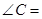 .
.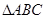 中,边
中,边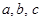 所对角分别为
所对角分别为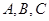 ,若
,若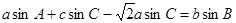 ,则
,则