题目内容
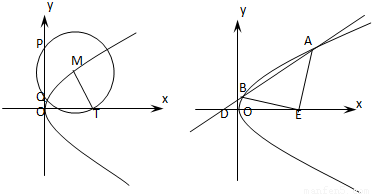
已知抛物线C:y2=4x.(1)设圆M过点T(2,0),且圆心M在抛物线C上,PQ是圆M在y轴上截得的弦,当点M在抛物线上运动时,弦长|PQ|是否为定值?说明理由;
(2)过点D(-1,0)的直线与抛物线C交于不同的两点A、B,在x轴上是否存在一点E,使△ABE为正三角形?若存在,求出E点坐标;若不存在,说明理由.
【答案】分析:(1)设圆心M( ,y),则圆半径r2=(
,y),则圆半径r2=( -2)2+y2,利用圆心M到y轴的距离结合直角三角形中的边的关系,即可求得弦长|PQ|为定值;
-2)2+y2,利用圆心M到y轴的距离结合直角三角形中的边的关系,即可求得弦长|PQ|为定值;
(2)设直线AB的方程为x=my-1,将直线的方程代入抛物线的方程,消去x得到关于y的一元二次方程,再结合根系数的关系利用垂直关系即可求得AB中垂线方程,从而得出△ABE为正三角形时的等式,即可解决问题.
解答:解:(1)设圆心M( ,y),则圆半径r2=(
,y),则圆半径r2=( -2)2+y2,
-2)2+y2,
圆心M到y轴的距离为d=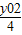 ,
,
∴弦长|PQ|=2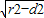
=2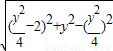 =2
=2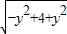 =4 (定值);
=4 (定值);
(2)设直线AB的方程为x=my-1,消x得y2-4my+4=0
△=16m2-16=16(m2-1)>0,∴m2>1,
∵y1+y2=4m,
∴AB的中点为N(2m2-1,2m),
∴AB中垂线方程为y-2m=-m(x-2m2+1),令y=0,∴x=2m2+1,
即E坐标为(2m2+1,0),
∴|EN|=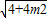 =2
=2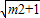 ,
,
又|AB|=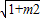 •4
•4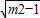 ,当△ABE为正三角形时,
,当△ABE为正三角形时,
|EN|=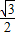 |AB|,∴2
|AB|,∴2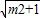 =
=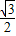 •
•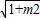 •4
•4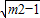 ,
,
∴m2= ,满足△>0,∴存在点E(
,满足△>0,∴存在点E( 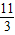 ,0).
,0).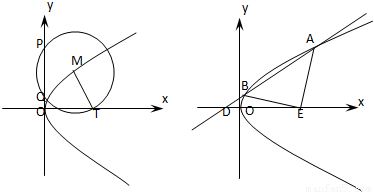
点评:本小题主要考查直线与圆锥曲线的关系、圆的方程、抛物线的方程及几何性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.
 ,y),则圆半径r2=(
,y),则圆半径r2=( -2)2+y2,利用圆心M到y轴的距离结合直角三角形中的边的关系,即可求得弦长|PQ|为定值;
-2)2+y2,利用圆心M到y轴的距离结合直角三角形中的边的关系,即可求得弦长|PQ|为定值;(2)设直线AB的方程为x=my-1,将直线的方程代入抛物线的方程,消去x得到关于y的一元二次方程,再结合根系数的关系利用垂直关系即可求得AB中垂线方程,从而得出△ABE为正三角形时的等式,即可解决问题.
解答:解:(1)设圆心M(
 ,y),则圆半径r2=(
,y),则圆半径r2=( -2)2+y2,
-2)2+y2,圆心M到y轴的距离为d=
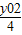 ,
,∴弦长|PQ|=2
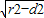
=2
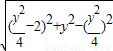 =2
=2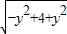 =4 (定值);
=4 (定值);(2)设直线AB的方程为x=my-1,消x得y2-4my+4=0
△=16m2-16=16(m2-1)>0,∴m2>1,
∵y1+y2=4m,
∴AB的中点为N(2m2-1,2m),
∴AB中垂线方程为y-2m=-m(x-2m2+1),令y=0,∴x=2m2+1,
即E坐标为(2m2+1,0),
∴|EN|=
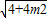 =2
=2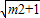 ,
,又|AB|=
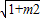 •4
•4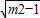 ,当△ABE为正三角形时,
,当△ABE为正三角形时,|EN|=
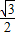 |AB|,∴2
|AB|,∴2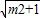 =
=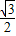 •
•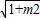 •4
•4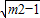 ,
,∴m2=
 ,满足△>0,∴存在点E(
,满足△>0,∴存在点E( 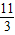 ,0).
,0).
点评:本小题主要考查直线与圆锥曲线的关系、圆的方程、抛物线的方程及几何性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点). 已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.
已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.