题目内容
从一个不透明的口袋中摸出红球的概率为1/5,已知袋中红球有3个,则袋中共有球的个数为( ).
| A.5个 | B.8个 | C.10个 | D.15个 |
D
由于从一个不透明的口袋中摸出红球的概率为1/5,并且袋中红球有3个,设袋中共有球的个数为n,则 所以
所以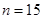 .
.
 所以
所以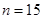 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
| A.5个 | B.8个 | C.10个 | D.15个 |
 所以
所以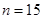 .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案