Question

已知函数f（x）=x²-2|x|．
（1）判断并证明函数的奇偶性；
（2）依图象写出函数的单调区间，并对函数f（x）在（-1，0）上的单调性加以证明．

Answer 1

（Ⅰ）函数是偶函数，定义域是R，
∵f（-x）=（-x）²-2|-x|=x²-2|x|=f（x），
∴函数f（x）是偶函数．
（Ⅱ）画出函数f（x）=

x2-2x，x≥0 x2+2x，x＜0

图象，
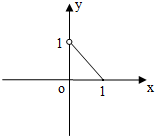
数形结合可得函数，如图：
单调递增区间为（-1，0），（1，+∞），
递减区间为（-∞，-1），（0，1）．
证明：当x∈（-1，0）时，∵f（x）=x²+2x，
设-1＜x₁＜x₂＜0，则x₁-x₂＜0，且x₁+x₂＞-2，即x₁+x₂+2＞0，
∵f(x1)-f(x2)=(

x

21

-

x

22

)+2(x1-x2)=（x₁-x₂）（x₁+x₂+2）＜0，
∴f（x₁）＜f（x₂），
所以，函数f（x）在（-1，0）上是单调递增函数．