题目内容
如图，正三棱锥P-ABC，PA＝4，AB＝2，D为BC中点，点E在AP上，满足AE＝3EP．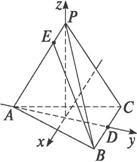
（1）建立适当坐标系，写出A、B、D、E四点的坐标；
（2）求异面直线AD与BE所成的角．
解：（1）建立如图坐标系：O为△ABC的重心，直线OP为z轴，AD为y轴，x轴平行于CB，得A（0，-
，0）、B（1，
，0）、D（0，
，0）、E（0，-
，
）．
（2）
=(0,
,0)，
=(-1,-
,
)，
设AD与BE所成的角为θ，则cosθ=
=
．
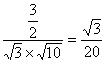∴θ=arccos
．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
如图，正三棱锥P-ABC的底面边长为1，E，F，G，H，分别是PA，AC，BC，PD的中点，四边形EFGH的面积为S（x），则S（x）值域为_________（ ）A、{
| ||||
B、（
| ||||
| C、（0，+∞） | ||||
D、（
|
如图，正三棱锥P-ABC的侧棱长为a，两侧棱PA、PC的夹角为30°，E、F分别是PA、PC上的动点，则△BEF的周长的最小值是（ ）
B．
C．
D．