题目内容
【题目】对于数列![]() ,把
,把![]() 作为新数列
作为新数列![]() 的第一项,把
的第一项,把![]() 或
或![]() (
(![]() )作为新数列
)作为新数列![]() 的第
的第![]() 项,数列
项,数列![]() 称为数列
称为数列![]() 的一个生成数列.例如,数列
的一个生成数列.例如,数列![]() 的一个生成数列是
的一个生成数列是![]() .已知数列
.已知数列![]() 为数列
为数列![]() 的生成数列,
的生成数列,![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)写出![]() 的所有可能值;
的所有可能值;
(2)若生成数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)证明:对于给定的![]() ,
,![]() 的所有可能值组成的集合为
的所有可能值组成的集合为![]() .
.
【答案】(1)![]() (2)
(2)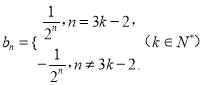 (3)详见解析.
(3)详见解析.
【解析】
试题(1)列举出数列![]() 所有可能情况,共
所有可能情况,共![]() 种,分别计算和值为
种,分别计算和值为![]() ,本题目的初步感观生成数列
,本题目的初步感观生成数列![]() (2)已知和项解析式,则可利用
(2)已知和项解析式,则可利用![]() 求通项. 当
求通项. 当![]() 时,
时,![]() ,而
,而![]() 当且仅当
当且仅当![]() 时,才成立.所以
时,才成立.所以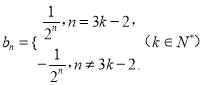 (3)本题实际是对(1)的推广.证明的实质是确定集合
(3)本题实际是对(1)的推广.证明的实质是确定集合![]() 的个数及其表示形式.首先集合
的个数及其表示形式.首先集合![]() 的个数最多有
的个数最多有![]() 种情形,而每一种的值都不一样,所以个数为
种情形,而每一种的值都不一样,所以个数为![]() 种情形,这是本题的难点,利用同一法证明. 确定集合
种情形,这是本题的难点,利用同一法证明. 确定集合![]() 的表示形式,关键在于说明分子为奇数.由
的表示形式,关键在于说明分子为奇数.由![]() 得分子必是奇数,奇数个数由范围
得分子必是奇数,奇数个数由范围![]() 确定.
确定.
试题解析:解:(1)由已知,![]() ,
,![]() ,
,
∴![]() ,
,
由于![]() ,
,
∴![]() 可能值为
可能值为![]() . 3分
. 3分
(2)∵![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,![]() , 5分
, 5分
∵![]() 是
是![]() 的生成数列,
的生成数列,
∴![]() ;
;![]() ;
;![]() ;
;
∴![]()
在以上各种组合中,
当且仅当![]() 时,才成立.
时,才成立.
∴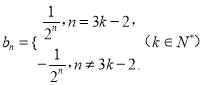 . 8分
. 8分
(3)![]() 共有
共有![]() 种情形.
种情形.
![]() ,即
,即![]() ,
,
又![]() ,分子必是奇数,
,分子必是奇数,
满足条件![]() 的奇数
的奇数![]() 共有
共有![]() 个. 10分
个. 10分
设数列![]() 与数列
与数列![]() 为两个生成数列,数列
为两个生成数列,数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,从第二项开始比较两个数列,设第一个不相等的项为第
,从第二项开始比较两个数列,设第一个不相等的项为第![]() 项.
项.
由于![]() ,不妨设
,不妨设![]() ,
,
则![]()
![]()
![]() ,
,
所以,只有当数列![]() 与数列
与数列![]() 的前
的前![]() 项完全相同时,才有
项完全相同时,才有![]() .12分
.12分
∴![]() 共有
共有![]() 种情形,其值各不相同.
种情形,其值各不相同.
∴![]() 可能值必恰为
可能值必恰为![]() ,共
,共![]() 个.
个.
即![]() 所有可能值集合为
所有可能值集合为![]() . 13分
. 13分
注:若有其它解法,请酌情给分】

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目