题目内容
已知函数
．（1）求f（x）的定义域和值域；
（2）证明函数
在（0，+∞）上是减函数．
【答案】分析：（1）根据使函数的解析式有意义的原则，我们易求出函数的解析式，根据反比例函数的性质，我们易求出函数的值域；
（2）任取区间（0，+∞）上两个任意的实数x1，x2，且x1＜x2，我们作差f（x1）-f（x2），并判断其符号，进而根据函数单调性的定义，可得到结论．
解答：解：（1）要使函数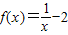
的解析式有意义
自变量应满足x≠0
故f（x）的定义域为（-∞，0）∪（0，+∞）
由于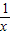
≠0，则
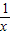-2≠-2
故f（x）的值域为（-∞，-2）∪（-2，+∞）
（2）任取区间（0，+∞）上两个任意的实数x1，x2，且x1＜x2，
则x1＞0，x2＞0，x2-x1＞0，
则f（x1）-f（x2）=（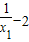
）-（
）=
-
=
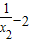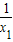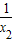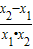＞0
即f（x1）＞f（x2）
故函数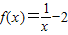
在（0，+∞）上是减函数
点评：本题考查的知识点是函数单调性的判断与证明，函数的定义域及其求法，函数的值域，其中熟练掌握基本初等函数的定义域，值域，及函数单调性的证明方法是解答本题的关键．
（2）任取区间（0，+∞）上两个任意的实数x1，x2，且x1＜x2，我们作差f（x1）-f（x2），并判断其符号，进而根据函数单调性的定义，可得到结论．
解答：解：（1）要使函数
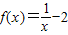的解析式有意义自变量应满足x≠0
故f（x）的定义域为（-∞，0）∪（0，+∞）
由于
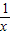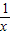≠0，则-2≠-2故f（x）的值域为（-∞，-2）∪（-2，+∞）
（2）任取区间（0，+∞）上两个任意的实数x1，x2，且x1＜x2，
则x1＞0，x2＞0，x2-x1＞0，
则f（x1）-f（x2）=（
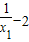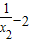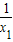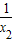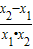）-（）=-=＞0即f（x1）＞f（x2）
故函数
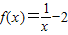在（0，+∞）上是减函数点评：本题考查的知识点是函数单调性的判断与证明，函数的定义域及其求法，函数的值域，其中熟练掌握基本初等函数的定义域，值域，及函数单调性的证明方法是解答本题的关键．
练习册系列答案
相关题目
．
．
的图象在x轴上方？
．
为f（x）的一个零点，求sin2x的值．
．
．
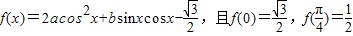，求f（x）的最大值和最小值．