题目内容
已知tan2θ=-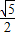
，且3π＜2θ＜4π．求：（1）tanθ；
（2）
．
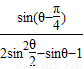【答案】分析：（1）由题意，可先判断角θ的取值范围，得出其是第四象限角从而确定出角的正切值的符号，再由正切的二倍角公式得到角的正切的方程，解此方程求出正切值；
（2）由题意，先化简
，再将tanθ=
代入计算出答案．
解答：解：（1）由题意3π＜2θ＜4π，得
＜θ＜2π是第四象限角
又tan2θ=-
，
∴
=-
，解得tanθ=
（2）由题，
将tanθ=
代入得
=
点评：本题考查二倍角的正切，二倍角的余弦，同角三角函数的基本关系等，解题的关键是利用公式灵活变形，计算求值，本题中有一易错点，即没有判断角所在的象限，导致解出的正切值有两个答案，切记！三角函数化简求值题，公式较多，要注意选择公式使得解题的过程简捷．本题考查了利用公式变形计算的能力．
（2）由题意，先化简
，再将tanθ=代入计算出答案．解答：解：（1）由题意3π＜2θ＜4π，得
＜θ＜2π是第四象限角又tan2θ=-
，∴
=-，解得tanθ=（2）由题，
将tanθ=
代入得=点评：本题考查二倍角的正切，二倍角的余弦，同角三角函数的基本关系等，解题的关键是利用公式灵活变形，计算求值，本题中有一易错点，即没有判断角所在的象限，导致解出的正切值有两个答案，切记！三角函数化简求值题，公式较多，要注意选择公式使得解题的过程简捷．本题考查了利用公式变形计算的能力．
练习册系列答案
相关题目