题目内容
已知tan2θ=-2| 2 |
(Ⅰ)求tanθ的值;
(Ⅱ)求
2cos2
| ||||
|
分析:(1)通过正切的倍角公式根据tan2θ求出tanθ的值.
(2)先用余弦的二倍角公式和两角和公式对原式进行化简,再把(1)中的tanθ代入即可得到答案.
(2)先用余弦的二倍角公式和两角和公式对原式进行化简,再把(1)中的tanθ代入即可得到答案.
解答:解:(1)∵tan2θ=
=-2
,
∴tanθ=-
或tanθ=
,
∵π<2θ<2π,
<θ<π,
∴tanθ=-
.
(2)原式=
=
=
=3+2
.
| 2tanθ |
| 1-tan2θ |
| 2 |
∴tanθ=-
| ||
| 2 |
| 2 |
∵π<2θ<2π,
| π |
| 2 |
∴tanθ=-
| ||
| 2 |
(2)原式=
| 1+cosθ-sinθ-1 |
| sinθ+cosθ |
| 1-tanθ |
| 1+tanθ |
1-(-
| ||||
1+(-
|
| 2 |
点评:本题主要考查三角函数中的两角和公式和倍角公式的运用.属基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
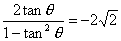 的值.
的值. ,π<2θ<2π,则tanθ的值为
,π<2θ<2π,则tanθ的值为
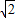 ,π<2θ<2π,则tanθ的值为( )
,π<2θ<2π,则tanθ的值为( )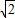
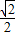
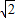 或-
或-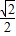
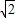 ,π<2θ<2π.
,π<2θ<2π.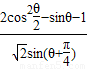 的值.
的值.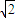 ,π<2θ<2π.
,π<2θ<2π.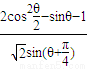 的值.
的值.