题目内容
已知圆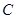 通过不同三点
通过不同三点 ,且直线
,且直线 斜率为
斜率为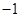 ,
,
(1)试求圆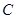 的方程;
的方程;
(2)若 是
是 轴上的动点,
轴上的动点,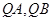 分别切圆
分别切圆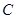 于
于 两点,
两点,
①求证:直线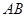 恒过一定点;
恒过一定点;
②求 的最小值.
的最小值.
(1)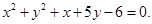 (2)①详见解析,②
(2)①详见解析,②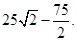
解析试题分析:(1)求圆的方程,基本方法为待定系数法.本题已知三点,宜设圆的一般式. 设圆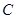 :
:
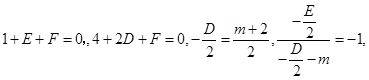
 (2)(1)证明切点弦恒过定点,关键将用参数表示切点弦方程,设
(2)(1)证明切点弦恒过定点,关键将用参数表示切点弦方程,设 ,则过
,则过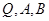 三点的圆是以
三点的圆是以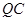 为直径的圆. 设为圆
为直径的圆. 设为圆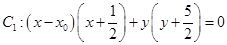 ①又因为圆
①又因为圆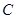 :
: ②,②-①得:
②,②-①得: ,
,



 恒过定点
恒过定点 (2)求
(2)求 的最小值,关键建立
的最小值,关键建立 函数关系式.本题设角为因变量,较为方便. 设
函数关系式.本题设角为因变量,较为方便. 设 则
则 则
则
 =
= =
= ,则
,则

 当
当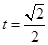 时,
时,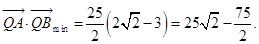
(1)设圆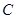 :
:
则 ,
,
即圆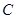 :
: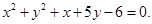 (也可以写成
(也可以写成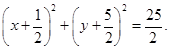 5分
5分
(2)(1)设 ,则过
,则过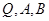 三点的圆是以
三点的圆是以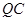 为直径的圆.
为直径的圆.
设为圆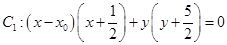 ①
①
又因为圆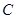 :
: ②
②
②-①得: ,
,



 恒过定点
恒过定点 10分
10分
设 则
则 则
则


= =
= ,
,
则

 当
当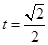 时,
时,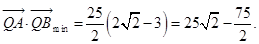 16分
16分
考点:圆的一般方程,圆的切点弦

练习册系列答案
相关题目
 与坐标轴交于点
与坐标轴交于点 .
.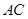 垂直的圆的切线方程;
垂直的圆的切线方程; 是圆上任意一点(不在坐标轴上),直线
是圆上任意一点(不在坐标轴上),直线 交
交 轴于点
轴于点 ,直线
,直线 交直线
交直线 ,
, ,求弦
,求弦 为定值.
为定值.
 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 在椭圆上,
在椭圆上, ,
, ,
, 的面积为
的面积为 .
. 轴上的圆,使圆在
轴上的圆,使圆在 轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
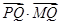 的最小值;
的最小值;
 ,求⊙O的半径r的长.
,求⊙O的半径r的长.
 ,且被圆C:
,且被圆C: 截得的弦长等于8的直线方程。
截得的弦长等于8的直线方程。 .
. 与圆
与圆 相切,且在
相切,且在 轴,
轴, 轴上的截距相等,求直线
轴上的截距相等,求直线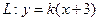 与圆
与圆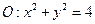 交于
交于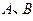 两点,则当
两点,则当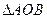 K*s^5#u的面积最大时,
K*s^5#u的面积最大时,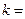 _______
_______