题目内容
已知圆 .
.
(1)已知不过原点的直线 与圆
与圆 相切,且在
相切,且在 轴,
轴, 轴上的截距相等,求直线
轴上的截距相等,求直线 的方程;
的方程;
(2)求经过原点且被圆 截得的线段长为2的直线方程.
截得的线段长为2的直线方程.
(1)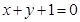 或
或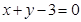 ;(2)
;(2)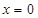 或
或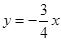 .
.
解析试题分析:(1)先设直线 的方程
的方程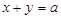 ,确定圆心
,确定圆心 的坐标及半径,进而由圆心
的坐标及半径,进而由圆心 到直线
到直线 的距离等于半径计算出参数
的距离等于半径计算出参数 的值,从而可写出直线
的值,从而可写出直线 的方程;(2)先检验所求直线的斜率不存在时,是否满足要求;然后设所求直线方程
的方程;(2)先检验所求直线的斜率不存在时,是否满足要求;然后设所求直线方程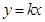 ,根据弦长为2,圆的半径
,根据弦长为2,圆的半径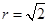 ,确定圆心到直线
,确定圆心到直线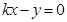 的距离
的距离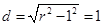 , 最后运用点到直线的距离公式得
, 最后运用点到直线的距离公式得 ,从中求解即可得到
,从中求解即可得到 ,进而写出直线的方程,最后综合两种情况写出所求的直线方程即可.
,进而写出直线的方程,最后综合两种情况写出所求的直线方程即可.
试题解析:(1)∵切线在两坐标轴上截距相等且不为零
设直线方程为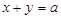 1分
1分
由圆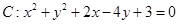 可得
可得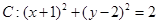
∴圆心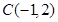 到切线的距离等于圆半径
到切线的距离等于圆半径 3分
3分
即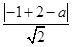 =
= 4分
4分
∴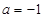 或
或 5分
5分
所求切线方程为: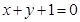 或
或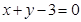 6分
6分
当直线斜率不存在时,直线即为 轴,此时,交点坐标为
轴,此时,交点坐标为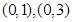 ,线段长为2,符合
,线段长为2,符合
故直线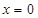 8分
8分
当直线斜率存在时,设直线方程为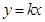 ,即
,即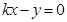
由已知得,圆心到直线的距离为1 9分
则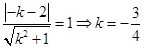 11分
11分
直线方程为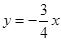
综上,直线方程为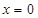 或
或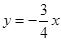 12分.
12分.
考点:1.直线与圆的位置关系;2.点到直线的距离公式;3.直线的方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
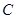 通过不同三点
通过不同三点 ,且直线
,且直线 斜率为
斜率为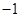 ,
, 是
是 轴上的动点,
轴上的动点,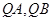 分别切圆
分别切圆 两点,
两点,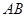 恒过一定点;
恒过一定点; 的最小值.
的最小值.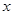 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切. 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围; 的直线
的直线 垂直平分弦
垂直平分弦 ?
? 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 的三个顶点
的三个顶点 ,
,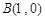 ,
,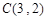 ,其外接圆为
,其外接圆为 .
. 过点
过点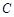 ,且被
,且被 上的任意一点
上的任意一点 ,若在以
,若在以 ,使得点
,使得点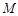 是线段
是线段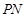 的中点,求
的中点,求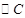 的半径
的半径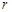 的取值范围.
的取值范围.