题目内容
【题目】已知奇函数 .
.
(1)求实数![]() 的值,并画出函数
的值,并画出函数![]() 的图象;
的图象;
(2)若函数![]() 在区间
在区间![]() 上是增函数,结合函数
上是增函数,结合函数![]() 的图象,求实数
的图象,求实数![]() 的取值范围;
的取值范围;
(3)结合图象,求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1) m=2. (2) (1,3].(3)最大值是1,最小值是-1.
【解析】
试题(1)根据奇函数定义得f(-x)=-f(x)代入可得m=2通过描点可得函数f(x)的图象;(2)根据图像可得[-1,a-2]为[-1,1]一个子集,结合数轴可得实数a满足的条件,解不等式可得a的取值范围(3)根据图像可得最高点与最低点,对应求出最大值和最小值.
试题解析:解:(1)当x<0时,-x>0,
则f(-x)=-(-x)2+2(-x)=-x2-2x.
又∵函数f(x)为奇函数,
∴f(-x)=-f(x).
∴f(x)=-f(-x)=-(-x2-2x)=x2+2x.
又∵当x<0时,f(x)=x2+mx,
∵对任意x<0,总有x2+2x=x2+mx,∴m=2.
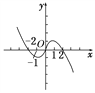
函数f(x)的图象如图所示.
(2)由(1)知f(x)=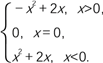
由图象可知,函数f(x)的图象在区间[-1,1]上的图象是“上升的”,
∴函数f(x)在区间[-1,1]上是增函数.
要使f(x)在[-1,a-2]上是增函数,
需有![]() 解得1<a≤3,
解得1<a≤3,
即实数a的取值范围是(1,3].
(3)由图象可知,函数f(x)的图象在区间[-2,2]上的最高点是(1,f(1)),最低点是(-1,f(-1)).
又因为f(1)=-1+2=1,f(-1)=1-2=-1,所以函数f(x)在区间[-2,2]上的最大值是1,最小值是-1.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们]对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15![]() 65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
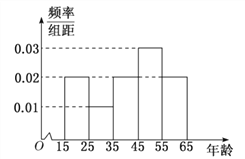
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | /td> | ||
总计 |
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.