题目内容
7.解关于x的不等式(1)${3}^{{x}^{2}-3x}$>34:
(2)a2x+1≥ax-5.
分析 (1)直接由指数函数的单调性化指数不等式为一元二次不等式求解;
(2)对a分类讨论,然后由指数函数的单调性化指数不等式为一元一次不等式求解.
解答 解:(1)由${3}^{{x}^{2}-3x}$>34,得x2-3x>4,解得:x<-1或x>4.
∴不等式${3}^{{x}^{2}-3x}$>34的解集为(-∞,-1)∪(4,+∞);
(2)当0<a<1时,由a2x+1≥ax-5,得
2x+1≤x-5,解得x≤-6;
当a>1时,由a2x+1≥ax-5,得
2x+1≥x-5,解得x≥-6.
∴当0<a<1时,原不等式的解集为(-∞,-6];
当a>1时,原不等式的解集为[6,+∞).
点评 本题考查指数不等式的解法,考查了指数函数的单调性,体现了分类讨论的数学思想方法,是基础题.

练习册系列答案
相关题目
18.若f(x)=ax2-$\sqrt{2}$(a>0),且f($\sqrt{2}$)=2,则a等于( )
| A. | 1+$\frac{\sqrt{2}}{2}$ | B. | 1-$\frac{\sqrt{2}}{2}$ | C. | 0 | D. | 2 |
12.若f(ex)=x,则f(e)=( )
| A. | 1 | B. | ee | C. | 2e | D. | 0 |
17.设全集U=R,A=(-∞,+∞),则∁UA=( )
| A. | ∅ | B. | R | C. | 不存在 | D. | (-∞,+∞) |
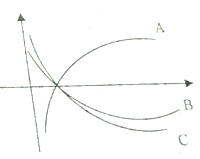 如图:下面三个分别是y=1og2x,y=${log}_{\frac{1}{3}}x$,y=log${\;}_{\frac{1}{4}}$x函数图象,则A代表函数y=1og2x; B代表函数y=log${\;}_{\frac{1}{4}}$x; C代表函数y=1og$\frac{1}{3}$x.
如图:下面三个分别是y=1og2x,y=${log}_{\frac{1}{3}}x$,y=log${\;}_{\frac{1}{4}}$x函数图象,则A代表函数y=1og2x; B代表函数y=log${\;}_{\frac{1}{4}}$x; C代表函数y=1og$\frac{1}{3}$x.