题目内容
已知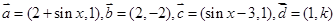 ,
,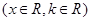
(1)若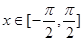 ,且
,且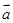 ∥(
∥(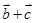 ),求x的值;
),求x的值;
(2)若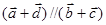 ,求实数
,求实数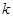 的取值范围.
的取值范围.
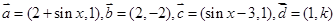 ,
,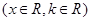
(1)若
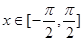 ,且
,且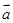 ∥(
∥(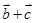 ),求x的值;
),求x的值;(2)若
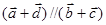 ,求实数
,求实数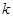 的取值范围.
的取值范围.(1) 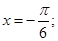 (2)
(2) 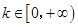 .
.
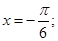 (2)
(2) 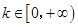 .
.试题分析:(1)先将向量
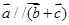 化为代数式,即
化为代数式,即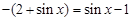 ,
,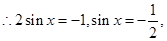
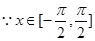 ;
;(2)由已知先写出
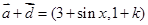 ,
,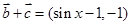 的坐标,再由
的坐标,再由 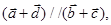 则有:
则有: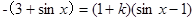 当
当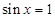 时等式不成立;将
时等式不成立;将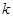 写成关于
写成关于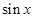 的函数,即
的函数,即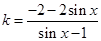 ,再求函数的值域即是
,再求函数的值域即是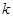 的取值范围为
的取值范围为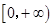
(或解)用
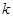 表示
表示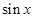 ,即
,即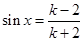 ,又因为
,又因为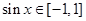 ,可解
,可解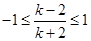 得
得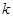 的取值范围为
的取值范围为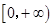 .
.试题解析:(1)
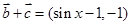 ,
,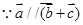 ,
, 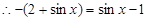 ,
,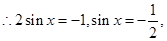
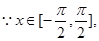
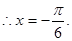
(2)
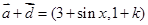 ,
,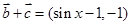
若
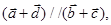 则有:
则有: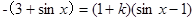
当
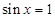 时等式不成立;
时等式不成立;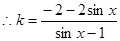 解得:
解得: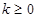
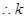 的取值范围为
的取值范围为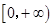

练习册系列答案
相关题目
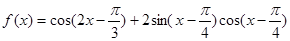 (
(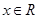 ).
).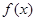 的最小正周期;
的最小正周期;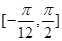 上的值域.
上的值域.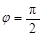 ”是“函数
”是“函数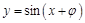 的图象关于y轴对称”的
的图象关于y轴对称”的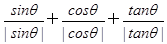 的值是( )
的值是( )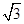 ).
).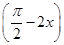 -2f2(x)在区间
-2f2(x)在区间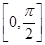 上的值域.
上的值域.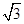 sin ωx+cos ωx(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间是________.
sin ωx+cos ωx(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间是________.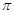
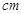 的弧所对的圆心角为
的弧所对的圆心角为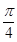 ,则这条弧所在的扇形面积为
,则这条弧所在的扇形面积为 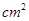 .
.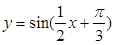 的图像可由函数
的图像可由函数 的图像( )
的图像( ) 个单位得到
个单位得到 个单位得到
个单位得到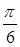 个单位得到
个单位得到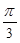 个单位得到
个单位得到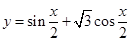 的图像的对称轴方程是 .
的图像的对称轴方程是 .