题目内容
【题目】甲船在岛![]() 的正南
的正南![]() 处,以4千米/时的速度向正北方向航行,
处,以4千米/时的速度向正北方向航行,![]() 千米,同时乙船自岛
千米,同时乙船自岛![]() 出发以6千米/时向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间为( )
出发以6千米/时向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间为( )
A.![]() B.
B.![]() C.
C.![]() D.2.15h
D.2.15h
【答案】A
【解析】
两船轨迹及距离最近时两船连线构成一个以![]() 岛为顶点,角度是
岛为顶点,角度是![]() 的三角形,设距离最近时航行时间为
的三角形,设距离最近时航行时间为![]() ,此时距离
,此时距离![]() ,此时甲船到
,此时甲船到![]() 岛距离为
岛距离为![]() ,乙船距离
,乙船距离![]() 岛
岛![]() ,
,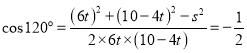 ,化简得:
,化简得:![]() ,由此能求出甲、乙两船相距最近时,航行的距离.
,由此能求出甲、乙两船相距最近时,航行的距离.
两船轨迹及距离最近时两船连线构成一个以![]() 岛为顶点,角度是
岛为顶点,角度是![]() 的三角形,
的三角形,
设距离最近时航行时间为![]() ,此时距离
,此时距离![]() ,
,
此时甲船到![]() 岛距离为
岛距离为![]() ,乙船距离
,乙船距离![]() 岛
岛![]() ,
,
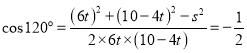 ,化简得:
,化简得:![]() ,
,
此函数的图像是抛物线,开口朝上,故在对称轴处![]() 有最小值,
有最小值,
故![]() 取最小值时,
取最小值时,![]() 小时,即
小时,即![]() .
.
故选:A

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
【题目】某小卖部为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数![]() 与当天气温(平均温度)
与当天气温(平均温度)![]() 的对比表:
的对比表:
| 0 | 1 | 3 | 4 |
| 140 | 136 | 129 | 125 |
(1)请在图中画出上表数据的散点图;

(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)如果某天的气温是![]() ,试根据(2)求出的线性回归方程预测这天大约可以卖出的热饮杯数.
,试根据(2)求出的线性回归方程预测这天大约可以卖出的热饮杯数.
参考公式:最小二乘法求线性回归方程系数公式: ,
,![]() .
.
参考数据:![]() .
.



