题目内容
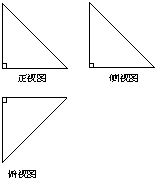 一个空间几何体的正视图、左视图、俯视图为全等的、直角边为1的等腰直角三角形(如图),那么这个几何体的体积为( )
一个空间几何体的正视图、左视图、俯视图为全等的、直角边为1的等腰直角三角形(如图),那么这个几何体的体积为( )| A、1 | ||
B、
| ||
C、
| ||
D、
|
分析:由三视图及题设条件知,此几何体为一个三棱锥,其高已知,底面是长度为1的等腰直角三角形,故先求出底面积,再由体积公式求解其体积即可.
解答:解:由题设条件,此几何几何体为一个三棱锥,其高已知为1,底面是长度为1的直角三角形,
底面积是
×1×1=
其体积是
×
×1=
故选D
底面积是
| 1 |
| 2 |
| 1 |
| 2 |
其体积是
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
故选D
点评:本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是.三视图的投影规则是:“主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等”.三视图是新课标的新增内容,在以后的高考中有加强的可能.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为2
如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为2| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 12、如图,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是直径为1的圆,那么这个几何体的侧面积为
12、如图,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是直径为1的圆,那么这个几何体的侧面积为
 (2012•长春模拟)一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的体积为( )
(2012•长春模拟)一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的体积为( ) 一个空间几何体的正视图、侧视图、俯视图如图所示,那么这个几何体的体积为
一个空间几何体的正视图、侧视图、俯视图如图所示,那么这个几何体的体积为