Question

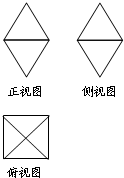
如图，一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形，如果直角三角形的斜边长为2

2

，那么这个几何体的体积为（　　）

• A、

  1

  3

• B、

  2

  3

• C、

  4

  3

• D、

  8

  3

Answer 1

分析：由三视图知几何体是一个三棱锥，三棱锥的底面是一个斜边长是2

2

的等腰直角三角形，做出底面的面积，垂直于底面的侧棱长是2，做出体积．

解答：解：由三视图知几何体是一个三棱锥，
三棱锥的底面是一个斜边长是2

2

的等腰直角三角形，
∴底面的面积是

1

2

×2×2=2
垂直于底面的侧棱长是2，
∴三棱锥的体积是

1

3

×2×2=

4

3

故选C．

点评：本题考查由三视图还原几何体并求几何体的体积，本题解题的关键是看出几何体的形状和长度，本题是一个基础题．