题目内容
(1)推导点到直线的距离公式;
(2)已知直线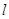 :
: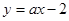 和
和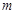 :
: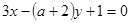 互相平行,求实数
互相平行,求实数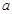 的值.
的值.
(1)详见解析;(2)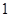 或
或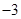
解析试题分析:(1)设点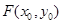 ,直线
,直线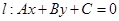 ,过点
,过点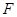 做直线
做直线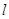 的垂线,垂足为
的垂线,垂足为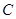 ,求出点
,求出点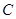 的坐标,在直线上在取不同于点
的坐标,在直线上在取不同于点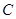 的一点
的一点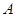 ,用两点间距离可求得
,用两点间距离可求得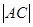 ,根据直角三角形中勾股定理可求得
,根据直角三角形中勾股定理可求得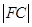 ,即点到直线的距离。(2)根据两直线平行斜率相等即可求出。
,即点到直线的距离。(2)根据两直线平行斜率相等即可求出。
试题解析:(1)(略) 6分
(2) ∥
∥ 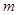 ,
, 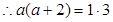 ,解得
,解得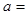 1或-3.
1或-3.
经检验均符合题意,故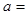 1或-3. 12分
1或-3. 12分
考点:1点到线的距离公式;2两直线平行时斜率的关系。

练习册系列答案
相关题目
设椭圆C1和抛物线C2的焦点均在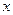 轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
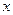 | 3 | -2 | 4 | 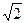 |
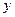 | 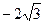 | 0 | -4 | 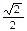 |
(1)求曲线C1,C2的标准方程;
(2)设直线
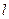 与椭圆C1交于不同两点M、N,且
与椭圆C1交于不同两点M、N,且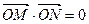 。请问是否存在直线
。请问是否存在直线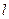 过抛物线C2的焦点F?若存在,求出直线
过抛物线C2的焦点F?若存在,求出直线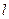 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.  的三个顶点
的三个顶点 (4,0),
(4,0),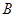 (8,10),
(8,10), (0,6).
(0,6).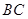 的直线方程;
的直线方程;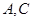 距离相等的直线方程。
距离相等的直线方程。 的顶点
的顶点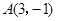 ,过点
,过点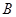 的内角平分线所在直线方程是
的内角平分线所在直线方程是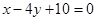 ,过点C的中线所在直线的方程是
,过点C的中线所在直线的方程是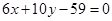
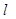 过点P(2,1),夹在两已知直线
过点P(2,1),夹在两已知直线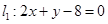 和
和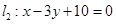 之间的线段AB恰被点P平分.
之间的线段AB恰被点P平分.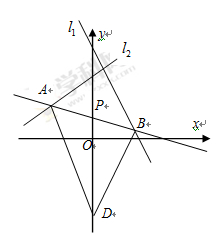
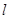 的方程;
的方程; ,求:
,求: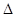 ABD的面积.
ABD的面积. ,1+
,1+