题目内容
12．在正三棱柱ABC-A1B1C1中，AB=a，D、E分别是BB1、CC1上的点，满足BC=EC=2BD，则平面ABC与平面ADE所成的二面角的大小为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 75° |
分析 由题意作图，并连结ED，CB交于点F，连结AF，从而可证明∠EAC即是平面ABC与平面ADE所成的二面角的平面角，从而求解．
解答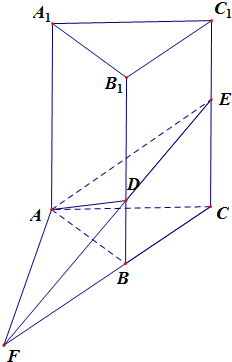 
解：由题意，连结ED，CB交于点F，连结AF，如右图，
∵BC=EC=2BD，
∴BD是△CEF的中位线，
∴BC=BF=AB=AC，
∴∠CAF=90°，
∴AC⊥AF，
又∵ABC-A1B1C1是正三棱柱，
∴∠EAC即是平面ABC与平面ADE所成的二面角的平面角，
又∵AC=CE，
∴∠EAC=45°，
故选B．
点评 本题考查了学生的作图能力及二面角的作法及大小的求法，属于中档题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
11．由不等式组$\left\{\begin{array}{l}{x+y≥1}\\{{e}^{x}-y≥0}\\{0≤x≤1}\end{array}\right.$确定的平面区域为M，由不等式组$\left\{{\begin{array}{l}{0≤x≤1}\\{0≤y≤e}\end{array}}\right.$确定的平面区域为N，在N内随机的取一点P，则点P落在区域M内的概率为（ ）
| A． | 1-$\frac{3}{e}$ | B． | 1-$\frac{2}{e}$ | C． | 1-$\frac{1}{e}$ | D． | 1-$\frac{3}{2e}$ |
如图，四棱锥P-ABCD的底面是正方形，PA⊥底面ABCD，PA=AD=2，点M，N分别为棱PD，PC的中点．